【答案】
分析:(1)根据已知得f′(-1)=0,得到a,利用导数研究函数的单调性的步骤求单调区间;
(2)把给定方程做适当的等价变换,得到g(x)的图象与x轴有3个交点;求出单调区间,求出函数的极值,依题意极大值大于0,极小值小于0,进而解出b的取值范围.
解答:解:(1)由已知得f′(x)=3x
2-6x+a,
∵在x=-1处的切线与x轴平行
∴f′(-1)=0,解得a=-9.
这时f′(x)=3x
2-6x-9=3(x+1)(x-3)
由f′(x)>0,解得x>3或x<-1;
由f′(x)<0,解-1<x<3.
∴f(x)的单调增区间为(-∞,-1)∪(3,+∞);单调减区间为(-1,3).
(2)令g(x)=f(x)-(

x
2-15x+3)=x
3-

x
2+6x+b-3
则原题意等价于g(x)图象与x轴有三个交点
∵g′(x)=3x
2-9x+6=3(x-1)(x-2)
∴由g′(x)>0,解得x>2或x<1;
由g′(x)<0,解得1<x<2.
∴g(x)在x=1时取得极大值g(1)=b-

;g(x)在x=2时取得极小值g(2)=b-1.
依题意得
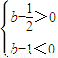
,解得

<b<1.
故b的取值范围为(

,1)
点评:本题考查导数的几何意义及利用导数研究函数的单调性,应熟练掌握利用可导函数研究函数的单调性的步骤.

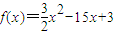 恰有三个不同的解,求b的取值范围.
恰有三个不同的解,求b的取值范围. x2-15x+3)=x3-
x2-15x+3)=x3- x2+6x+b-3
x2+6x+b-3 ;g(x)在x=2时取得极小值g(2)=b-1.
;g(x)在x=2时取得极小值g(2)=b-1.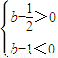 ,解得
,解得 <b<1.
<b<1. ,1)
,1)

 名校课堂系列答案
名校课堂系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<