
已知数列{an}为等差数列,公差为d,若 <-1,且它的前n项和Sn有最大值,则使得Sn<0的n的最小值为( )
<-1,且它的前n项和Sn有最大值,则使得Sn<0的n的最小值为( )
(A)11(B)19(C)20(D)21
C
【解析】【思路点拨】解答本题首先要搞清条件“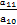 <-1”及“Sn有最大值”如何使用,从而列出关于a1,d的不等式组,求出
<-1”及“Sn有最大值”如何使用,从而列出关于a1,d的不等式组,求出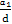 的取值范围,进而求出使得Sn<0的n的最小值,或者根据等比数列的性质求解.
的取值范围,进而求出使得Sn<0的n的最小值,或者根据等比数列的性质求解.
解:方法一:由题意知d<0,a10>0,a11<0, a10+a11<0,
由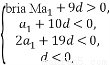 得-
得-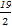 <
<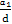 <-9.
<-9.
∵Sn=na1+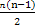 d=
d=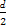 n2+(a1-
n2+(a1-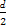 )n,
)n,
由Sn=0得n=0或n=1-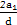 .
.
∵19<1-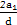 <20,
<20,
∴Sn<0的解集为{n∈N*|n>1-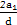 },
},
故使得Sn<0的n的最小值为20.
方法二:由题意知d<0,a10>0,a11<0,a10+a11<0,
由a10>0知S19>0,由a11<0知S21<0,
由a10+a11<0知S20<0,故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十三第三章第七节练习卷(解析版) 题型:解答题
在△ABC中,角A,B,C所对的边分别为a,b,c,且cosA= .
.
(1)求sin2 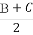 -cos 2A的值.
-cos 2A的值.
(2)若a=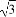 ,求bc的最大值.
,求bc的最大值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十第五章第一节练习卷(解析版) 题型:解答题
数列{an}满足:a1=1,an+1=3an+2n+1(n∈N*),求{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十第五章第一节练习卷(解析版) 题型:选择题
已知数列{an}中,a1=1,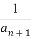 =
= +3(n∈N*),则a10=( )
+3(n∈N*),则a10=( )
(A)28(B)33(C)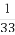 (D)
(D)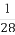
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十四第五章第五节练习卷(解析版) 题型:填空题
设数列{an}中,a1=2,an+1=an+n+1,则通项an= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十四第五章第五节练习卷(解析版) 题型:选择题
等差数列{an}的公差为3,若a2, a4,a8成等比数列,则a4=( )
(A)8 (B)10 (C)12 (D)16
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十六第六章第二节练习卷(解析版) 题型:选择题
已知不等式xy≤ax2+2y2,若对任意x∈[1,2]及y∈[2,3],该不等式恒成立,则实数a的范围是( )
(A)-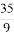 ≤a≤-1 (B)-3≤a≤-1
≤a≤-1 (B)-3≤a≤-1
(C)a≥-3 (D)a≥-1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十八第六章第四节练习卷(解析版) 题型:选择题
已知a>0,b>0,a+b=2,则 +
+ 的最小值是( )
的最小值是( )
(A) (B)4 (C)
(B)4 (C) (D)5
(D)5
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:解答题
某少数民族的刺绣有着悠久的历史,如图(1)(2)(3)(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
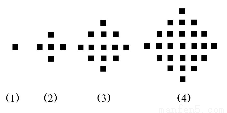
(1)求出f(5).
(2)利用合情推理的“归纳推理思想”归纳出f(n+1)与f(n)的关系式,并根据你得到的关系式求f(n)的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com