
| A. | (2$\sqrt{2}$,$\frac{π}{4}$) | B. | (2$\sqrt{2}$,$\frac{3π}{4}$) | C. | (2,$\frac{π}{4}$) | D. | (2,$\frac{3π}{4}$) |
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 阅读程序框图,并完成下列问题:
阅读程序框图,并完成下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
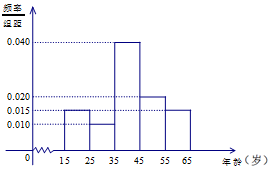 电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.
电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数. | 观看方式 年龄(岁) | 电视 | 网络 |
| [15,45) | 150 | 250 |
| [45,65] | 120 | 80 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,3) | B. | (-2,3] | C. | (0,3) | D. | (0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com