
(本题14分)对于函数 ,若
,若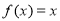 ,则称
,则称 为
为 的“不动点”,若
的“不动点”,若 ,则称
,则称 为
为 的“稳定点”,函数
的“稳定点”,函数 的“不动点”和“稳定点”的集合分别记为A和B,即
的“不动点”和“稳定点”的集合分别记为A和B,即 .
.
(1)设 ,求集合A和B;
,求集合A和B;
(2)若 ,
, ,求实数
,求实数 的取值范围;
的取值范围;
(3)若 ,求证:
,求证: .
.
(1) ,
, ;(2)
;(2) ;
;
【解析】
试题分析:(1)紧扣题中给出的“不动点”和“稳定点”的定义,准确列出关于 的方程,求得集合A和B;(2)利用“不动点”和“稳定点”的定义,分别讨论参数
的方程,求得集合A和B;(2)利用“不动点”和“稳定点”的定义,分别讨论参数 和
和 两种情况且注意分母不能为0,求出集
两种情况且注意分母不能为0,求出集 和
和 ,再由
,再由 ,确定
,确定 的取值范围;(3)利用“不动点”和“稳定点”的定义,分别讨论参数
的取值范围;(3)利用“不动点”和“稳定点”的定义,分别讨论参数 和
和 两种情况,求出集
两种情况,求出集 和
和 ,证得结论.本题属于创新型问题,在求解时关键在于准确把握新定义,正确应用新定义和相关知识求解所给的问题,要在理解新定义上下功夫,在应用新定义解决所给问题上做文章.具体到本题中,函数
,证得结论.本题属于创新型问题,在求解时关键在于准确把握新定义,正确应用新定义和相关知识求解所给的问题,要在理解新定义上下功夫,在应用新定义解决所给问题上做文章.具体到本题中,函数 的“不动点”本质就是方程
的“不动点”本质就是方程 的解,函数
的解,函数 的“稳定点”本质就是方程
的“稳定点”本质就是方程 的解,只要能牢牢把握这一本质,就能解好本题目.
的解,只要能牢牢把握这一本质,就能解好本题目.
试题解析:(1)由 ,得
,得 ,解得
,解得 ; 1分
; 1分
由 ,得
,得 ,解得
,解得 . 2分
. 2分
所以集合 ,
, . 4分
. 4分
(2)①若 ,则
,则 ,符合题意; 5分
,符合题意; 5分
②若 ,由题意有:
,由题意有: ,
,
注意: ,验证得:
,验证得: 不是方程
不是方程 的根;
的根;
∴ ; 6分
; 6分
 ,
,
注意:
 且
且 ,
,
验证得: 和
和 都不是方程
都不是方程 的根,
的根,
∴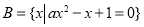 ; 8分
; 8分
∴ ;∵
;∵ ,∴
,∴ ,∴方程
,∴方程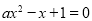 有解,
有解,
∴
 且
且 ; 9分
; 9分
综上,实数 的取值范围是
的取值范围是 . 10分
. 10分
(3)①若 ,
, ,结论成立; 11分
,结论成立; 11分
②若 ,由
,由 得
得 ,则
,则 12分
12分
∵
考虑方程: ,∵
,∵ ,∴方程
,∴方程 无解.
无解.
∴ ; 13分
; 13分
∴ . 14分
. 14分
考点:①含参数的一元二次方程解法;②集合与集合的关系.


科目:高中数学 来源:2014-2015学年江西省高一上学期第一次月考数学试卷(解析版) 题型:选择题
设函数
 ,若
,若 ,
, ,则关于
,则关于 的方程
的方程 的解的个数为( )
的解的个数为( )
(A)1 (B)2 (C)3 (D)4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省吉安市高一上学期第一次段考数学试卷(解析版) 题型:填空题
已知集合A=B=R, ,
, ,
, ,若4和10的原象分别是6和9,则19在
,若4和10的原象分别是6和9,则19在 作用下的象为 。
作用下的象为 。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省吉安市高一上学期第一次段考数学试卷(解析版) 题型:选择题
定义集合运算: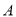 ※
※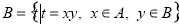 ,设
,设 ,
, ,则集合A※B的所有元素之和为( )
,则集合A※B的所有元素之和为( )
A.6 B.3 C.2 D.0
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省高二上学期第一次月考文科数学试卷(解析版) 题型:选择题
不等式x(2﹣x)≤ 0的解集为( )
0的解集为( )
A.{x|0≤x≤2} B.{x|x≤0或x≥2} C.{x|x≤2} D.{x|x≥0}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com