D
分析:令f(x+2)-f(x)≤3×2
x (1),f(x+6)-f(x)≥63×2
x (2),(1)-(2)可得f(x+2)-f(x+6)≤-60×2
x (3),再由(1)可得f(x+2)-f(x+6)≥-60×2
x (7),由(3)和(7)得到,f(x+2)-f(x+6)=-60×2
x(8),再对(1)变形联立(2)可得f(x+6)=f(x)+63×2
x,与(8)联立得 f(x+2)-f(x)=3×2
x,利用累加法及等比数列求和即可求得f(2012).
解答:f(x+2)-f(x)≤3×2
x (1),f(x+6)-f(x)≥63×2
x (2),
由 (1)-(2)得到,f(x+2)-f(x+6)≤3×2
x-63×2
x=-60×2
x,
所以,f(x+2)-f(x+6)≤-60×2
x (3),
由(1)得,f(x+6)-f(x+4)≤3×2
x+4=48×2
x (5),
f(x+4)-f(x+2)≤3×2
x+2=12×2
x (6),
由(5)+(6)得到,f(x+6)-f(x+2)≤60×2
x,即f(x+2)-f(x+6)≥-60×2
x (7),
由(3)和(7)得到,f(x+2)-f(x+6)=-60×2
x(8),
由(1)得,f(x+6)≤f(x+4)+3×2
x+4≤f(x+2)+3×2
x+2+3×2
x+4≤f(x)+3×2
x+3×2
x+2+2
x+4=f(x)+63×2
x,
又由(2)知,f(x+6)=f(x)+63×2
x,与(8)联立得 f(x+2)-f(x)=3×2
x,
所以f(x+2)=f(x)+3•2
x,
所以 f(2012)=f(2010)+3×2
2010,
f(2010)=f(2008)+3×2
2008,…
f(2)=f(0)+3×2
0,
等式两边同时相加得到f(2012)=f(0)+3×2
2010+3×2
2008+…+3×2
0=2012+3×(2
2010+2
2008+…+2
0),
等比数列求和得f(2012)=2012+3×
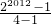
=2012+2
2012-1=2011+2
2012.
故选D
点评:本题考查不等式、等比数列求和等知识,考查学生分析解决问题的能力,本题综合性强,难度大,对能力要求高.

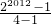 =2012+22012-1=2011+22012.
=2012+22012-1=2011+22012.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案