解:(1)过
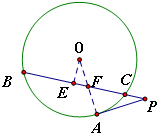
O作OE⊥BC于E,连接OA,交AB于F
∵PA与圆O切于A点,
∴PA
2=PC•PB,即(2

)
2=1•PB,得PB=12
∴AB=PB-PC=11,可得BE=

BC=5.5
∵PA与圆O切于A点,
∴OA⊥PA,得Rt△PAF中,AF=PAtan30°=2,PF=2AF=4
∵Rt△OEF中,∠OFE=∠PFA=90°-30°=60°,EF=PB-BE-PF=2.5
∴OF=
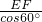
=5,可得圆O的半径为R=OF+AF=7
(2)点A(
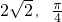
)化成直角坐标为A(2,2),而圆C:ρ=4sinθ的直角坐标方程是x
2+y
2-4y=0
∵2
2+2
2-4×2=0
∴点A(2,2)适合圆C方程,得点A是圆C上的点
∵圆C的圆心为(0,2),得AC的斜率k=
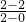
=0,
∴过A与AC垂直的直线为x=2,即为过A点与圆C相切的直线
因此切线的极坐标方程是ρcosθ=2
故答案为:7 ρcosθ=2
分析:(1)过O作OE⊥BC于E,连接OA,交AB于F.由切割线定理,得PA
2=PC•PB,求得PB=12,再结合垂直于弦的直径,得到BE=

BC=5.5,然后在Rt△PAF中,算出AF=PAtan30°=2,PF=2AF=4,最后在Rt△OEF中算出OF=5,即可得到圆O的半径为7;
(2)将极坐标化成直角坐标,得到已知点恰好在已知圆上,利用切线垂直于过切点的半径,可得到切线的直角坐标方程,最后将此方程化成极坐标方程即可.
点评:本题给出圆的切线长和割线长求圆的半径,并且在已知直线与圆的极坐标的情况下求切线的方程,着重考查了与圆有关系的比例线段和简单曲线的极坐标方程等知识,属于中档题.

 ,PC=1,则圆O的半径等于________.
,PC=1,则圆O的半径等于________.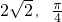 )作圆ρ=4sinθ的切线,则切线的极坐标方程是________.
)作圆ρ=4sinθ的切线,则切线的极坐标方程是________. O作OE⊥BC于E,连接OA,交AB于F
O作OE⊥BC于E,连接OA,交AB于F )2=1•PB,得PB=12
)2=1•PB,得PB=12 BC=5.5
BC=5.5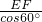 =5,可得圆O的半径为R=OF+AF=7
=5,可得圆O的半径为R=OF+AF=7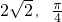 )化成直角坐标为A(2,2),而圆C:ρ=4sinθ的直角坐标方程是x2+y2-4y=0
)化成直角坐标为A(2,2),而圆C:ρ=4sinθ的直角坐标方程是x2+y2-4y=0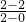 =0,
=0, BC=5.5,然后在Rt△PAF中,算出AF=PAtan30°=2,PF=2AF=4,最后在Rt△OEF中算出OF=5,即可得到圆O的半径为7;
BC=5.5,然后在Rt△PAF中,算出AF=PAtan30°=2,PF=2AF=4,最后在Rt△OEF中算出OF=5,即可得到圆O的半径为7;

 选做题:请考生在下列两题中任选一题作答,若两题都做,则按所做的第一题评阅计分.
选做题:请考生在下列两题中任选一题作答,若两题都做,则按所做的第一题评阅计分.