
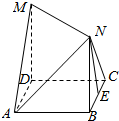
 如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD且MD=NB=1,E为BC的中点
如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD且MD=NB=1,E为BC的中点分析 (1)以D为坐标原点,DA、DC、DM所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出异面直线NE与AM所成角的余弦值.
(2)假设在线段AN上存在点F,使FE与平面AMN所成角为30°,设$\overrightarrow{AF}$=$λ\overrightarrow{AN}$=(0,λ,λ),(0≤λ≤1),利用向量法推导出$λ=\frac{2±3\sqrt{2}}{4}$与0≤λ≤1矛盾,从而在线段AN上不存在点F,使得FE与平面AMN所成角为30°.
解答 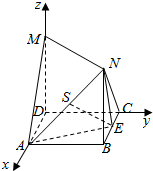 解:(1)如图,以D为坐标原点,DA、DC、DM所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,
解:(1)如图,以D为坐标原点,DA、DC、DM所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,
则D(0,0,0),A(1,0,0),M(0,0,1),
C(0,1,0),B(1,1,0),N(1,1,1),E($\frac{1}{2}$,1,0),
∴$\overrightarrow{NE}=(-\frac{1}{2},0,-1)$,$\overrightarrow{AM}$=(-1,0,1),
∵$\overrightarrow{NE}$=(-$\frac{1}{2}$,0,-1),$\overrightarrow{AM}$=(-1,0,1),
∵|cos<$\overrightarrow{NE},\overrightarrow{AM}$>|=$\frac{|\overrightarrow{NE}•\overrightarrow{AM}|}{|\overrightarrow{NE}|•|\overrightarrow{AM}|}$=$\frac{\frac{1}{2}}{\sqrt{\frac{5}{4}}•\sqrt{2}}$=$\frac{\sqrt{10}}{10}$,
∴异面直线NE与AM所成角的余弦值为$\frac{\sqrt{10}}{10}$.
(2)不存在F,使EF与平面AMN所成角为30°,
假设在线段AN上存在点F,使FE与平面AMN所成角为30°,
设$\overrightarrow{AF}$=$λ\overrightarrow{AN}$=(0,λ,λ),(0≤λ≤1),
又$\overrightarrow{EA}$=($\frac{1}{2},-1,0$),∴$\overrightarrow{EF}$=$\overrightarrow{EA}+\overrightarrow{AF}$=($\frac{1}{2},λ-1,λ$),
设平面AMN的一个法向量$\overrightarrow{n}$=(x,y,z),
$\overrightarrow{AM}$=(-1,0,1),$\overrightarrow{AN}$=(0,1,1),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AM}=-x+z=0}\\{\overrightarrow{n}•\overrightarrow{AN}=y+z=0}\end{array}\right.$,取z=1,得$\overrightarrow{n}$=(1,-1,1),
∵点F使得FE与平面AMN所成角为30°,
∴sin30°=|cos<$\overrightarrow{EF},\overrightarrow{n}$>|=$\frac{\frac{3}{2}}{\sqrt{\frac{1}{4}+(λ-1)^{2}+{λ}^{2}}•\sqrt{3}}$=$\frac{1}{2}$,
解得$λ=\frac{2±3\sqrt{2}}{4}$与0≤λ≤1矛盾,
∴在线段AN上不存在点F,使得FE与平面AMN所成角为30°.
点评 本题考查异面直线所成角的余弦值的求法,考查使得线面角为30°的点是否存在的判断与证明,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
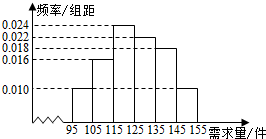 某商场经销某一种电器商品,在一个销售季度内,每售出一件该商品获利200元,未售出的商品,每件亏损100元,根据以往资料,得到销售季度内市场需求量的频率分布直方图,如图所示,现在经销商为下一个销售季度购进了125件该种电器,以n(单位:件;95≤n≤155)表示下一个销售季度市场需求量,Y(单位:元)表示下一个销售季度内销售 该电器的利润.
某商场经销某一种电器商品,在一个销售季度内,每售出一件该商品获利200元,未售出的商品,每件亏损100元,根据以往资料,得到销售季度内市场需求量的频率分布直方图,如图所示,现在经销商为下一个销售季度购进了125件该种电器,以n(单位:件;95≤n≤155)表示下一个销售季度市场需求量,Y(单位:元)表示下一个销售季度内销售 该电器的利润.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com