
【题目】设n≥2,n∈N* , 有序数组(a1 , a2 , …,an)经m次变换后得到数组(bm , 1 , bm , 2 , …,bm , n),其中b1 , i=ai+ai+1 , bm , i=bm﹣1 , i+bm﹣1 , i+1(i=1,2,…,n),an+1=a1 , bm﹣1 , n+1=bm﹣1 , 1(m≥2).例如:有序数组(1,2,3)经1次变换后得到数组(1+2,2+3,3+1),即(3,5,4);经第2次变换后得到数组(8,9,7).
(1)若ai=i(i=1,2,…,n),求b3 , 5的值;
(2)求证:bm , i= ![]() ai+jCmj , 其中i=1,2,…,n. (注:i+j=kn+t时,k∈N* , i=1,2,…,n,则ai+j=a1)
ai+jCmj , 其中i=1,2,…,n. (注:i+j=kn+t时,k∈N* , i=1,2,…,n,则ai+j=a1)
【答案】
(1)解:依题意(1,2,3,4,5,6,7,8,…,n),
第一次变换为(3,5,7,9,11,13,15,…,n+1),
第二次变换为(8,12,16,20,24,28,…,n+4),
第三次变换为(20,28,36,44,52,…,n+12),
∴b3,5=52
(2)解:用数学归纳法证明:对m∈N*,bm,i= ![]() ai+jCmj,其中i=1,2,…,n,
ai+jCmj,其中i=1,2,…,n,
(i)当m=1时,b1,i= ![]() ai+jC1j,其中i=1,2,…,n,结论成立,
ai+jC1j,其中i=1,2,…,n,结论成立,
(ii)假设m=k时,k∈N*时,bk,i= ![]() ai+jCkj,其中i=1,2,…,n,
ai+jCkj,其中i=1,2,…,n,
则m=k+1时,bk+1,i=bk,i+bk,i+1= ![]() ai+jCkj+
ai+jCkj+ ![]() ai+j+1Ckj=
ai+j+1Ckj= ![]() ai+jCkj+
ai+jCkj+ ![]() ai+j+1Ckj﹣1,
ai+j+1Ckj﹣1,
=aiCk0+ ![]() ai+j(Ckj+Ckj﹣1)+ai+k+1Ckk,
ai+j(Ckj+Ckj﹣1)+ai+k+1Ckk,
=aiCk+10+ ![]() ai+jCk+1j+ai+k+1Ck+1k+1,
ai+jCk+1j+ai+k+1Ck+1k+1,
= ![]() ai+jCk+1j,
ai+jCk+1j,
所以结论对m=k+1时也成立,
由(i)(ii)可知,对m∈N*,bm,i= ![]() ai+jCmj,其中i=1,2,…,n成立
ai+jCmj,其中i=1,2,…,n成立
【解析】(1)根据新定义,分别进行1次,2次,3次变化,即可求出答案,(2)利用数学归纳法证明即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知美国苹果公司生产某款iphone手机的年固定成本为40万美元,每生产1只还需另投入16美元.设苹果公司一年内共生产该款iphone手机x万只并全部销售完,每万只的销售收入为R(x)万美元,且R(x)= 
(1)写出年利润W(万元)关于年产量x(万只)的函数解析式;
(2)当年产量为多少万只时,苹果公司在该款手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,直线
,直线![]() .
.
(1)求与圆![]() 相切,且与直线
相切,且与直线![]() 垂直的直线方程;
垂直的直线方程;
(2)在直线![]() 上(
上(![]() 为坐标原点),存在定点
为坐标原点),存在定点![]() (不同于点
(不同于点![]() ),满足:对于圆
),满足:对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:
(1)设所求直线方程为![]() ,利用圆心到直线的距离等于半径可得关于b的方程,解方程可得
,利用圆心到直线的距离等于半径可得关于b的方程,解方程可得![]() ,则所求直线方程为
,则所求直线方程为![]()
(2)方法1:假设存在这样的点![]() ,由题意可得
,由题意可得![]() ,则
,则![]() ,然后证明
,然后证明![]() 为常数
为常数![]() 为即可.
为即可.
方法2:假设存在这样的点![]() ,使得
,使得![]() 为常数
为常数![]() ,则
,则![]() ,据此得到关于
,据此得到关于![]() 的方程组,求解方程组可得存在点
的方程组,求解方程组可得存在点![]() 对于圆
对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为常数
为常数![]() .
.
试题解析:
(1)设所求直线方程为![]() ,即
,即![]() ,
,
∵直线与圆相切,∴![]() ,得
,得![]() ,
,
∴所求直线方程为![]()
(2)方法1:假设存在这样的点![]() ,
,
当![]() 为圆
为圆![]() 与
与![]() 轴左交点
轴左交点![]() 时,
时,![]() ;
;
当![]() 为圆
为圆![]() 与
与![]() 轴右交点
轴右交点![]() 时,
时,![]() ,
,
依题意,![]() ,解得,
,解得,![]() (舍去),或
(舍去),或![]() .
.
下面证明点![]() 对于圆
对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为一常数.
为一常数.
设![]() ,则
,则![]() ,
,
∴![]()
![]()
![]() ,
,
从而![]() 为常数.
为常数.
方法2:假设存在这样的点![]() ,使得
,使得![]() 为常数
为常数![]() ,则
,则![]() ,
,
∴![]() ,将
,将![]() 代入得,
代入得,
![]() ,即
,即
![]() 对
对![]() 恒成立,
恒成立,
∴![]() ,解得
,解得 或
或![]() (舍去),
(舍去),
所以存在点![]() 对于圆
对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为常数
为常数![]() .
.
点睛:求定值问题常见的方法有两种:
(1)从特殊入手,求出定值,再证明这个值与变量无关.
(2)直接推理、计算,并在计算推理的过程中消去变量,从而得到定值.
【题型】解答题
【结束】
22
【题目】已知函数![]() 的导函数为
的导函数为![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() 时,求
时,求![]() 的最大值,并推断方程
的最大值,并推断方程![]() 是否有实数解;
是否有实数解;
(2)若![]() 在区间
在区间![]() 上的最大值为-3,求
上的最大值为-3,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作
作![]() 的垂线与以
的垂线与以![]() 为直径的圆
为直径的圆![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)若![]() ,求圆
,求圆![]() 的方程;
的方程;
(2)求证:点![]() 始终在某定圆上.
始终在某定圆上.
(3)是否存在一定点![]() (异于点
(异于点![]() ),使得
),使得![]() 为常数?若存在,求出定点
为常数?若存在,求出定点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某机械厂要将长![]() ,宽
,宽![]() 的长方形铁皮
的长方形铁皮![]() 进行裁剪.已知点
进行裁剪.已知点![]() 为
为![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,裁剪时先将四边形
上,裁剪时先将四边形![]() 沿直线
沿直线![]() 翻折到
翻折到![]() 处(点
处(点![]() 分别落在直线
分别落在直线![]() 下方点
下方点![]() 处,
处,![]() 交边
交边![]() 于点
于点![]() ),再沿直线
),再沿直线![]() 裁剪.
裁剪.

(1)当![]() 时,试判断四边形
时,试判断四边形![]() 的形状,并求其面积;
的形状,并求其面积;
(2)若使裁剪得到的四边形![]() 面积最大,请给出裁剪方案,并说明理由.
面积最大,请给出裁剪方案,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x﹣a,g(x)=x+2.
(1)当a=1时,求不等式f(x)+f(﹣x)≤g(x)的解集;
(2)求证: ![]() 中至少有一个不小于
中至少有一个不小于 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)的两个焦点与短轴的一个端点是直角三角形的3个顶点,直线l:y=﹣x+3与椭圆E有且只有一个公共点T.
=1(a>b>0)的两个焦点与短轴的一个端点是直角三角形的3个顶点,直线l:y=﹣x+3与椭圆E有且只有一个公共点T.
(Ⅰ)求椭圆E的方程及点T的坐标;
(Ⅱ)设O是坐标原点,直线l′平行于OT,与椭圆E交于不同的两点A、B,且与直线l交于点P.证明:存在常数λ,使得|PT|2=λ|PA||PB|,并求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 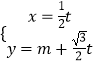 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2﹣2ρcosθ﹣4=0
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2﹣2ρcosθ﹣4=0
(1)若直线l与曲线C没有公共点,求m的取值范围;
(2)若m=0,求直线l被曲线C截得的弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com