
分析 利用两角和公式对等式左边进行展开,化简整理,进而利用同角三角函数基本关系,进一步化简整理可得:原式=(cosα)2-(sinβ)2,结合已知即可得解.
解答 解:∵cos(α+β)cos(α-β)=$\frac{2}{5}$,
∴cos(α+β)cos(α-β)
=(cosαcosβ-sinαsinβ)•(cosαcosβ+sinαsinβ)
=(cosαcosβ)2-(sinαsinβ)2
=(cosα)2[1-(sinβ)2]-(sinβ)2[1-(cosα)2]
=(cosα)2-(sinβ)2
∴sin2β-cos2α=-$\frac{2}{5}$.
故答案为:-$\frac{2}{5}$.
点评 本题主要考查了两角和与差的余弦函数.考查了学生对基础知识的掌握,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | (0,2) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,0]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知P是圆C:(x+1)2+y2=16.上任意一点,A(1,0),线段PA的垂直平分线与PC相交于点Q.
已知P是圆C:(x+1)2+y2=16.上任意一点,A(1,0),线段PA的垂直平分线与PC相交于点Q.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
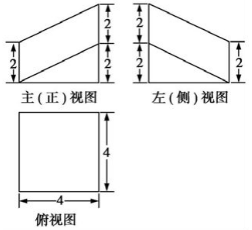
| A. | 32+8$\sqrt{6}$ | B. | 48+8$\sqrt{6}$ | C. | 48+8$\sqrt{3}$ | D. | 44+8$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com