
| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
分析 根据双曲线的定义和方程确定a,c的值,结合余弦定理以及向量数量积的定义进行计算即可.
解答 解:由双曲线定义得,||PF1|-|PF2||=8,|F1F2|=10,
${|{{F_1}{F_2}}|^2}={|{P{F_1}}|^2}+{|{P{F_2}}|^2}-2|{P{F_1}}|•|{P{F_2}}|cos∠{F_1}P{F_2}$,
可得|PF1|•|PF2|=36,
∴$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=|{\overrightarrow{P{F_1}}}|•|{\overrightarrow{P{F_2}}}|cos\frac{π}{3}=18$,
故选D.
点评 本题主要考查向量数量积的应用以及双曲线的定义的应用,利用余弦定理结合双曲线的定义建立方程是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 过定点(0,1) | B. | 过定点(0,2) | C. | 过定点(a,1) | D. | 过定点(a,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | [-2,+∞) | C. | (-3,+∞) | D. | (-$\frac{9}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,侧面PAB⊥底面ABCD,PA=2$\sqrt{2}$,PB=2.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,侧面PAB⊥底面ABCD,PA=2$\sqrt{2}$,PB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<1} | B. | {-1,0,1} | C. | {-1,0} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
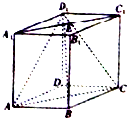 已知四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD为菱形.
已知四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD为菱形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥$\frac{1}{2}$ | B. | m≥2 | C. | 0<m<$\frac{1}{2}$ | D. | 0<m≤$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 休闲方式 性别 | 逛街 | 上网 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com