
| A. | $\sqrt{3}$ | B. | 9 | C. | 81 | D. | $27\sqrt{3}$ |
分析 作出满足约束条件$\left\{\begin{array}{l}2x-y+1≤0\\ x-2y-1≥0\end{array}$的可行域,数形结合,再由指数函数的图象和性质,可得z=27-x•$\frac{1}{{3}^{y}}$的最小值.
解答 解:作出满足约束条件$\left\{\begin{array}{l}2x-y+1≤0\\ x-2y-1≥0\end{array}$的可行域如下图所示:
其中P点坐标为(-1,-1),
由z=27-x•$\frac{1}{{3}^{y}}$=3-3x-y,
令t=-3x-y,
则当直线t=-3x-y过P点时,t取最小值-4,
此时z=27-x•$\frac{1}{{3}^{y}}$的最小值为81,
故选:C
点评 本题考查的知识点是简单的线性规划,指数函数的图象和性质,难度中档.


科目:高中数学 来源: 题型:解答题
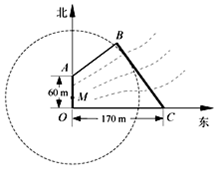 如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=$\frac{4}{3}$.
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=$\frac{4}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,以A为原点建立空间直角坐标系A-xyz后,B(3,0,0),D(0,4,0),A1(0,0,5),E(3,3,3),一质点从A点出发,沿直线向E点运动,然后会依次被长方体ABCD-A1B1C1D1的各个面反弹(符合反射定律),
如图,以A为原点建立空间直角坐标系A-xyz后,B(3,0,0),D(0,4,0),A1(0,0,5),E(3,3,3),一质点从A点出发,沿直线向E点运动,然后会依次被长方体ABCD-A1B1C1D1的各个面反弹(符合反射定律),查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{\sqrt{3}}{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7\sqrt{2}}{2}$ | B. | $\sqrt{29}$ | C. | 5 | D. | 以上都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2-\sqrt{3}}}{2}$ | B. | $\frac{{2-\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}-1}}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {l,2,3} | C. | {0} | D. | {1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com