
ЁОЬтФПЁПУЄКаРяУцЭЈГЃзАЕФЪЧЖЏТўЁЂгАЪгзїЦЗЕФжмБпЃЌЛђепЩшМЦЪІЕЅЖРЩшМЦГіРДЕФЭцХМ.гЩгкКазгЩЯУЛгаБъзЂЃЌЙКТђепжЛгаДђПЊВХЛсжЊЕРздМКТђЕНСЫЪВУДЃЌвђДЫетжжОЊЯВЮќв§СЫжкЖрФъЧсШЫЃЌаЮГЩСЫЁАУЄКаОМУЁБ.ФГПюУЄКаФкПЩФмзАгаФГвЛЬзЭцХМЕФ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§жжбљЪНЃЌЧвУПИіУЄКажЛзАвЛИі.
Ш§жжбљЪНЃЌЧвУПИіУЄКажЛзАвЛИі.
ЃЈ1ЃЉШєУПИіУЄКазАга![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§жжбљЪНЭцХМЕФИХТЪЯрЭЌ.ФГЭЌбЇвбОгаСЫ
Ш§жжбљЪНЭцХМЕФИХТЪЯрЭЌ.ФГЭЌбЇвбОгаСЫ![]() бљЪНЕФЭцХМЃЌШєЫћдйЙКТђСНИіетПюУЄКаЃЌЧЁКУФмЪеМЏЦыетШ§жжбљЪНЕФИХТЪЪЧЖрЩйЃП
бљЪНЕФЭцХМЃЌШєЫћдйЙКТђСНИіетПюУЄКаЃЌЧЁКУФмЪеМЏЦыетШ§жжбљЪНЕФИХТЪЪЧЖрЩйЃП
ЃЈ2ЃЉФГЯњЪлЭјЕуЮЊЕїВщИУПюУЄКаЕФЪмЛЖгГЬЖШЃЌЫцЛњЗЂЗХСЫ200ЗнЮЪОэЃЌВЂШЋВПЪеЛи.ОЭГМЦЃЌга![]() ЕФШЫЙКТђСЫИУПюУЄКаЃЌдкетаЉЙКТђепЕБжаЃЌХЎЩњеМ
ЕФШЫЙКТђСЫИУПюУЄКаЃЌдкетаЉЙКТђепЕБжаЃЌХЎЩњеМ![]() ЃЛЖјдкЮДЙКТђепЕБжаЃЌФаЩњХЎЩњИїеМ
ЃЛЖјдкЮДЙКТђепЕБжаЃЌФаЩњХЎЩњИїеМ![]() .ЧыИљОнвдЩЯаХЯЂЬюаДЯТБэЃЌВЂЗжЮіЪЧЗёга
.ЧыИљОнвдЩЯаХЯЂЬюаДЯТБэЃЌВЂЗжЮіЪЧЗёга![]() ЕФАбЮеШЯЮЊЙКТђИУПюУЄКагыадБ№гаЙиЃП
ЕФАбЮеШЯЮЊЙКТђИУПюУЄКагыадБ№гаЙиЃП
ХЎЩњ | ФаЩњ | змМЦ | |
ЙКТђ | |||
ЮДЙКТђ | |||
змМЦ |
ВЮПМЙЋЪНЃК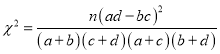 ЃЌЦфжа
ЃЌЦфжа![]() .
.
span>ВЮПМЪ§ОнЃК
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ЃЈ3ЃЉИУЯњЪлЭјЕувбОЪлТєИУПюУЄКа6жмЃЌВЂМЧТМСЫЯњЪлЧщПіЃЌШчЯТБэЃК
жмЪ§ | 1 | 2 | 3 | 4 | 5 | 6 |
КаЪ§ | 16 | ______ | 23 | 25 | 26 30 |
гЩгкЕчФдЙЪеЯЃЌЕкЖўжмЪ§ОнЯжвбЖЊЪЇЃЌИУЯњЪлЭјЕуИКд№ШЫОіЖЈгУЕк4ЁЂ5ЁЂ6жмЕФЪ§ОнЧѓЯпадЛиЙщЗНГЬЃЌдйгУЕк1ЁЂ3жмЪ§ОнНјааМьбщ.
ЂйЧыгУ4ЁЂ5ЁЂ6жмЕФЪ§ОнЧѓГі![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬ
ЕФЯпадЛиЙщЗНГЬ![]() ЃЛ
ЃЛ
ЃЈзЂЃК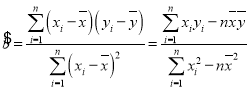 ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЂкШєгЩЯпадЛиЙщЗНГЬЕУЕНЕФЙРМЦЪ§ОнгыЫљбЁГіЕФМьбщЪ§ОнЕФЮѓВюОљВЛГЌЙ§2КаЃЌдђШЯЮЊЕУЕНЕФЯпадЛиЙщЗНГЬЪЧПЩППЕФЃЌЪдЮЪЂйжаЫљЕУЕФЯпадЛиЙщЗНГЬЪЧЗёПЩППЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЬюБэМћНтЮіЃЌга
ЃЛЃЈ2ЃЉЬюБэМћНтЮіЃЌга![]() АбЮеШЯЮЊЁАЙКТђИУПюУЄКагыадБ№гаЙиЁБЃЛЃЈ3ЃЉЂй
АбЮеШЯЮЊЁАЙКТђИУПюУЄКагыадБ№гаЙиЁБЃЛЃЈ3ЃЉЂй![]() ЃЛЂкПЩПП.
ЃЛЂкПЩПП.
ЁОНтЮіЁП
ЃЈ1ЃЉСаОйГіЛљБОЪТМўЕФзмЪ§КЭЪТМўЁАЫћЧЁКУФмЪеМЏЦыетШ§жжбљЪНЁБЫљАќКЌЕФЛљБОЪТМўЕФИіЪ§ЃЌРћгУЙХЕфИХаЭЕФИХТЪМЦЫуЙЋЪНЃЌМДПЩЧѓНт.
ЃЈ2ЃЉИљОнЬтвтЃЌЕУГі![]() ЕФСаСЊБэЃЌРћгУЙЋЪНЧѓЕУ
ЕФСаСЊБэЃЌРћгУЙЋЪНЧѓЕУ![]() ЕФжЕЃЌНсКЯИНБэЃЌМДПЩЕУЕННсТлЃЛ
ЕФжЕЃЌНсКЯИНБэЃЌМДПЩЕУЕННсТлЃЛ
ЃЈ3ЃЉЂйЧѓЕУ![]() ЕФжЕЃЌИљОнЙЋЪНЧѓЕУ
ЕФжЕЃЌИљОнЙЋЪНЧѓЕУ![]() ЕФжЕЃЌЧѓЕУЛиЙщжБЯпЗНГЬЃЛЂкЕБ
ЕФжЕЃЌЧѓЕУЛиЙщжБЯпЗНГЬЃЛЂкЕБ![]() КЭ
КЭ![]() ЪБЃЌБШНЯМДПЩЕУЕННсТл.
ЪБЃЌБШНЯМДПЩЕУЕННсТл.
ЃЈ1ЃЉгЩЬтвтЃЌЛљБОЪТМўПеМфЮЊ
![]() ЃЌЦфжаЛљБОЪТМўЕФИіЪ§ЮЊ9ИіЃЌ
ЃЌЦфжаЛљБОЪТМўЕФИіЪ§ЮЊ9ИіЃЌ
ЩшЪТМў![]() ЮЊЃКЁАЫћЧЁКУФмЪеМЏЦыетШ§жжбљЪНЁБЃЌдђ
ЮЊЃКЁАЫћЧЁКУФмЪеМЏЦыетШ§жжбљЪНЁБЃЌдђ![]() ЃЌ
ЃЌ
ЦфжаЛљБОЪТМўЕФИіЪ§ЮЊ2ЃЌ
ЫљвдЫћЧЁКУФмЪеМЏЦыетШ§жжбљЪНЕФИХТЪ![]() .
.
ЃЈ2ЃЉ
ХЎЩњ | ФаЩњ | змМЦ | |
ЙКТђ | 40 | 20 | 60 |
ЮДЙКТђ | 70 | 70 | 140 |
змМЦ | 110 | 90 | 200 |
дђ![]() .
.
гжвђЮЊ![]() ЃЌЙЪга
ЃЌЙЪга![]() АбЮеШЯЮЊЁАЙКТђИУПюУЄКагыадБ№гаЙиЁБ.
АбЮеШЯЮЊЁАЙКТђИУПюУЄКагыадБ№гаЙиЁБ.
ЃЈ3ЃЉЂйгЩЪ§ОнЃЌЧѓЕУ![]() ЃЌ
ЃЌ![]() .
.
гЩЙЋЪНЧѓЕУ![]() ЃЌ
ЃЌ
![]() .
.
Ыљвд![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬЮЊ
ЕФЯпадЛиЙщЗНГЬЮЊ![]() .
.
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЭЌбљЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() .
.
ЫљвдЃЌЫљЕУЕНЕФЯпадЛиЙщЗНГЬЪЧПЩППЕФ.


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШє![]() ЃЌЕБxЁЪ[0ЃЌ1]ЪБЃЌfЃЈxЃЉЃНxЃЌШєдкЧјМфЃЈЉ1ЃЌ1]ФкЃЌ
ЃЌЕБxЁЪ[0ЃЌ1]ЪБЃЌfЃЈxЃЉЃНxЃЌШєдкЧјМфЃЈЉ1ЃЌ1]ФкЃЌ![]() гаСНИіСуЕуЃЌдђЪЕЪ§mЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
гаСНИіСуЕуЃЌдђЪЕЪ§mЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХзЪБОЪаГЁЕФЧПЪЦНјШыЃЌЛЅСЊЭјЙВЯэЕЅГЕЁАКіШчвЛвЙДКЗчРДЁБЃЌБщВМСЫИїМЖГЧЪаЕФДѓНжаЁЯяЃЌЮЊСЫНтЮвЪаЕФЪаУёЖдЙВЯэЕЅГЕЕФТњвтЖШЃЌФГЕїВщЛњЙЙНшжњЭјТчНјааСЫЮЪОэЕїВщЃЌВЂДгВЮгыЕїВщЕФЭјгбжаЫцЛњГщШЁСЫ50ШЫНјааЗжЮіЃЎШєЕУЗжЕЭгк60ЗжЃЌЫЕУїВЛТњвтЃЌШєЕУЗжВЛЕЭгк60ЗжЃЌЫЕУїТњвтЃЌЕїВщТњвтЖШЕУЗжЧщПіНсЙћгУОЅвЖЭМБэЪОШчЭМ1ЃЎ
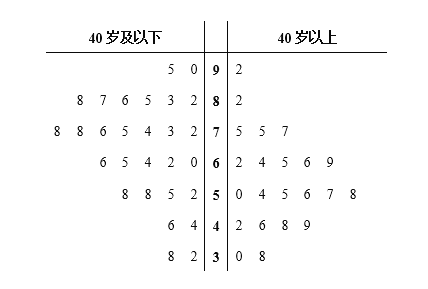
ЃЈЂёЃЉИљОнОЅвЖЭМевГі40ЫъвдЩЯЭјгбжаТњвтЖШЕУЗжЕФжкЪ§КЭжаЮЛЪ§ЃЛ
ЃЈЂђЃЉИљОнОЅвЖЭМЭъГЩЯТУцСаСЊБэЃЌВЂИљОнвдЩЯЪ§ОнЃЌХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊТњвтЖШгыФъСфгаЙиЃЛ
ЕФАбЮеШЯЮЊТњвтЖШгыФъСфгаЙиЃЛ
Тњвт | ВЛТњвт | КЯМЦ | |
40ЫъвдЯТ | |||
40ЫъвдЩЯ | |||
КЯМЦ |
ЃЈЂѓЃЉЯШВЩгУЗжВуГщбљЕФЗНЗЈДг40ЫъМАвдЯТЕФЭјгбжабЁШЁ7ШЫЃЌдйДгет7ШЫжаЫцЛњбЁГі2ШЫЃЌНЋЦЕТЪЪгЮЊИХТЪЃЌЧѓбЁГіЕФ2ШЫжажСЩйга1ШЫЪЧВЛТњвтЕФИХТЪЃЎ
ВЮПМИёЪНЃК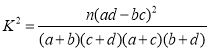 ЃЌЦфжа
ЃЌЦфжа![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙѕзгЪЧПЭМвДЋЭГХЉОпЃЌФЯЗНХЉУёРчПЊЬяЕиКѓЃЌШдгаДѓЕФЭСПщ.ХЉШЫБугУСљЦЌвЖГнзщГЩЙѕжсЃЌСНВрзАЩЯФОАхЃЌШЫПчПЊСННХеОСЂЃЌМШФмеЦЮеЦНКтЃЌгжФмдіМгжиСПЃЌШУХЃРЖЏЙѕжсЧАНјЃЌбЙЫщЭСПщЃЌвдРћгкИћжж.етСљЦЌвЖГнгжЖдгІзХЦаШјСљЖШЃЌМДВМЪЉГжНфШЬШшОЋНјьјЖЈгыАуШє.ШєМзввУПШЫвРДЮгаЗХЛиЕиДгетСљЦЌвЖГнжаЫцЛњШЁвЛЦЌЃЌдђетСНШЫбЁЕФвЖГнЖдгІЕФЁАЖШЁБЯрЭЌЕФИХТЪЮЊ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§![]() .
.
ЃЈ1ЃЉЬжТл![]() ЕФЕЅЕїадЃЛ
ЕФЕЅЕїадЃЛ
ЃЈ2ЃЉШє![]() гаСНИіМЋжЕЕу
гаСНИіМЋжЕЕу![]() ЃЌ
ЃЌ![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
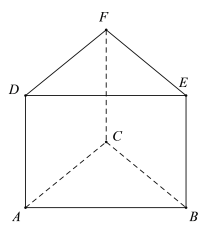
ЁОЬтФПЁПШчЭМЃЌдке§ЗНЬх![]() жаЃЌЕу
жаЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФЖЏЕуЃЌдђЯТСаЫЕЗЈе§ШЗЕФЪЧ______ЃЈЬюађКХЃЉ
ЩЯЕФЖЏЕуЃЌдђЯТСаЫЕЗЈе§ШЗЕФЪЧ______ЃЈЬюађКХЃЉ
ЂйЮоТлЕу![]() дк
дк![]() ЩЯдѕУДвЦЖЏЃЌЖМга
ЩЯдѕУДвЦЖЏЃЌЖМга![]() ЃЛ
ЃЛ
ЂкЮоТлЕу![]() дк
дк![]() ЩЯдѕУДвЦЖЏЃЌвьУцжБЯп
ЩЯдѕУДвЦЖЏЃЌвьУцжБЯп![]() гы
гы![]() ЫљГЩНЧЖМВЛПЩФмЪЧ
ЫљГЩНЧЖМВЛПЩФмЪЧ![]() ЃЛ
ЃЛ
ЂлЕБЕу![]() вЦЖЏжС
вЦЖЏжС![]() жаЕуЪБЃЌжБЯп
жаЕуЪБЃЌжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧзюДѓЃЛ
ЫљГЩНЧзюДѓЃЛ
ЂмЕБЕу![]() вЦЖЏжС
вЦЖЏжС![]() жаЕуЪБЃЌВХга
жаЕуЪБЃЌВХга![]() гы
гы![]() ЯрНЛгквЛЕуЃЌМЧЮЊЕу
ЯрНЛгквЛЕуЃЌМЧЮЊЕу![]() ЃЌЧв
ЃЌЧв![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§![]() ЃЌ
ЃЌ![]() ЃЌЦфжаГЃЪ§
ЃЌЦфжаГЃЪ§![]() .
.
ЃЈ1ЃЉШєКЏЪ§![]() гы
гы![]() гаЯрЭЌЕФМЋжЕЕуЃЌЧѓ
гаЯрЭЌЕФМЋжЕЕуЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШє![]() ЃЌХаЖЯКЏЪ§
ЃЌХаЖЯКЏЪ§![]() гы
гы![]() ЭМЯѓЕФНЛЕуИіЪ§.
ЭМЯѓЕФНЛЕуИіЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
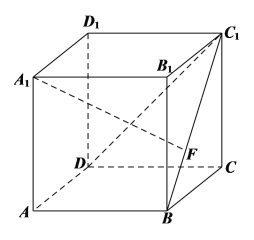
ЁОЬтФПЁПЖрУцЬх![]() жаЃЌЁї
жаЃЌЁї![]() ЮЊЕШБпШ§НЧаЮЃЌЁї
ЮЊЕШБпШ§НЧаЮЃЌЁї![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЮЊЕШбќжБНЧШ§НЧаЮЃЌ![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() ЦНУц
ЦНУц![]() .
.
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓЦНУц
ЃЌЧѓЦНУц![]() гыЦНУц
гыЦНУц![]() ЫљГЩЕФНЯаЁЕФЖўУцНЧЕФгрЯвжЕ.
ЫљГЩЕФНЯаЁЕФЖўУцНЧЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() Й§зјБъдЕуOЧвгыдВ
Й§зјБъдЕуOЧвгыдВ![]() ЯрНЛгкЕуAЃЌBЃЌдВMЙ§ЕуAЃЌBЧвгыжБЯп
ЯрНЛгкЕуAЃЌBЃЌдВMЙ§ЕуAЃЌBЧвгыжБЯп![]() ЯрЧаЃЎ
ЯрЧаЃЎ
ЃЈ1ЃЉЧѓдВаФMЕФЙьМЃCЕФЗНГЬЃЛ
ЃЈ2ЃЉШєдВаФдкxжсе§АыжсЩЯУцЛ§ЕШгк![]() ЕФдВWгыЧњЯпCгаЧвНіга1ИіЙЋЙВЕуЃЎ
ЕФдВWгыЧњЯпCгаЧвНіга1ИіЙЋЙВЕуЃЎ
ЃЈЂЁЃЉЧѓГідВWБъзМЗНГЬЃЛ
ЃЈЂЂЃЉвбжЊаБТЪЕШгк![]() ЕФжБЯп
ЕФжБЯп![]() ЃЌНЛЧњЯпCгкEЃЌFСНЕуЃЌНЛдВWгкPЃЌQСНЕуЃЌЧѓ
ЃЌНЛЧњЯпCгкEЃЌFСНЕуЃЌНЛдВWгкPЃЌQСНЕуЃЌЧѓ![]() ЕФзюаЁжЕМАДЫЪБжБЯп
ЕФзюаЁжЕМАДЫЪБжБЯп![]() ЕФЗНГЬЃЎ
ЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com