
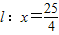 的距离之比为
的距离之比为 的点的轨迹方程为
的点的轨迹方程为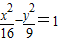 ;
;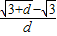 无限趋近于
无限趋近于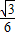 ;
;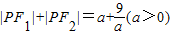 ,则点P的轨迹为椭圆;
,则点P的轨迹为椭圆;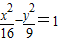 的右焦点为(5,0),右准线为x=
的右焦点为(5,0),右准线为x=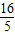 ,离心率e=
,离心率e= ,根据圆锥曲线的定义可判断
,根据圆锥曲线的定义可判断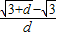 =
=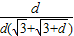 =
=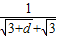 可判断
可判断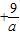 ≥6=F1F2,满足
≥6=F1F2,满足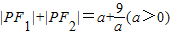 ≥F1F2,根据椭圆定义可判断
≥F1F2,根据椭圆定义可判断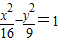 的右焦点为(5,0),右准线为x=
的右焦点为(5,0),右准线为x=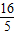 ,离心率e=
,离心率e= ,根据圆锥曲线的定义可知,和定点A(5,0)及定直线x=
,根据圆锥曲线的定义可知,和定点A(5,0)及定直线x=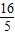 的距离之比为
的距离之比为 的点的轨迹方程为
的点的轨迹方程为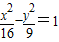 ;错误
;错误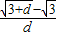 =
=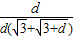 =
=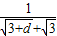 无限趋近于
无限趋近于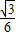 ;正确
;正确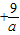 ≥6=F1F2,根据椭圆的定义可知,P满足
≥6=F1F2,根据椭圆的定义可知,P满足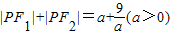 ,则点P的轨迹为椭圆或线段,故错误
,则点P的轨迹为椭圆或线段,故错误

科目:高中数学 来源: 题型:
|
|
|
|
| A、①④ | B、②③ | C、①③ | D、②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 6 |
| π |
| 2 |
| 2 |
| sinθ |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
①m![]() α,n
α,n![]() β,m∥n
β,m∥n![]() α∥β;②m
α∥β;②m![]() α,n
α,n![]() β,m∥β,n∥α
β,m∥β,n∥α![]() α∥β;③m⊥α,n⊥β,m∥n
α∥β;③m⊥α,n⊥β,m∥n![]() α∥β;④AB∥α,AC∥α
α∥β;④AB∥α,AC∥α![]() 平面ABC∥α.其中正确的是( )
平面ABC∥α.其中正确的是( )
A.①② B.①②③ C.②③ D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)n=n+l;
(2)2n>2n+1(n≥3);
(3)2+4+6+…+2n=n2+n+2;
(4)凸n边形对角线的条数f(n)=![]() .
.
其中满足“假设n=k(k∈N*,k≥n0)时命题成立,则当n=k+1时命题也成立”,但不满足“当n=n0(n0是题中给定的n的初始值)时命题成立”的命题序号是________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com