
分析 (1)利用对数的运算性质即可求解;(2)解简单对数的对数方程,通常把两边化成同底的对数式,从而转化为真数相等,问题得解.注意真数要大于零.
解答 解:(1)原式=-5$lo{g}_{3}2+lo{g}_{3}\frac{32}{9}-{5}^{lo{g}_{6}3}-[(\frac{1}{4})^{3}]^{\frac{2}{3}}$
=$lo{g}_{3}{(2}^{-5}×\frac{32}{9})-{5}^{lo{g}_{6}3}-\frac{1}{16}$
=$-2-{5}^{lo{g}_{6}3}-\frac{1}{16}$
=-$\frac{33}{16}-{5}^{lo{g}_{6}3}$.
故计算结果为$\frac{33}{16}-{5}^{lo{g}_{6}3}$.
(2)∵$lo{g}_{3}({6}^{x}-9)=3$,即$lo{g}_{3}({6}^{x}-9)=lo{g}_{3}{3}^{3}$,
∴6x-9=27,
∴6x=36,
∴x=6.
故方程的解为x=3.
点评 本题考查对数运算的性质和简单的对数方程.考查对对数的运算性质的掌握和运算能力.基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
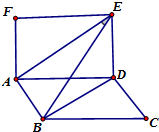 如图,矩形ADEF和矩形ABCD有公共边AD.
如图,矩形ADEF和矩形ABCD有公共边AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,+∞) | C. | (-2,$\frac{1}{2}$] | D. | [$\frac{1}{2}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{435600}$-$\frac{{y}^{2}}{564400}$=1(x>0) | B. | $\frac{{x}^{2}}{64{0}^{2}}$-$\frac{{y}^{2}}{48{0}^{2}}$=1(x>0) | ||
| C. | $\frac{{x}^{2}}{435600}$+$\frac{{y}^{2}}{564400}$=1 | D. | $\frac{{x}^{2}}{64{0}^{2}}$+$\frac{{y}^{2}}{48{0}^{2}}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5或6 | B. | 6 | C. | 5 | D. | 4或5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com