
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(2)若函数![]() 为
为![]() 上的单调函数,求实数
上的单调函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 得
得![]() ,对其求导,得到
,对其求导,得到![]() ,解对应不等式,求出单调区间,进而可求出最值;
,解对应不等式,求出单调区间,进而可求出最值;
(2)先由![]() 得到函数
得到函数![]() 不可能在
不可能在![]() 上单调递增,由题意,得到
上单调递增,由题意,得到![]() 在
在![]() 上单调递减,推出
上单调递减,推出![]() 恒成立;令
恒成立;令![]() ,用导数的方研究其单调性,进而可求出结果.
,用导数的方研究其单调性,进而可求出结果.
(1)当![]() 时,
时,![]() ,所以
,所以![]() .
.
由![]() 解得
解得![]() ,由
,由![]() 解得
解得![]() .
.
故函数![]() 在区间
在区间![]() 上单减,在区间
上单减,在区间![]() 上单增.
上单增.
![]() ,
,
![]() ,
,![]() ;
;
(2) 因为![]() ,所以函数
,所以函数![]() 不可能在
不可能在![]() 上单调递增.
上单调递增.
所以,若函数![]() 为
为![]() 上单调函数,则必是单调递减函数,即
上单调函数,则必是单调递减函数,即![]() 恒成立.
恒成立.
由![]() 可得
可得![]() ,
,
故![]() 恒成立的必要条件为
恒成立的必要条件为![]() .
.
令![]() ,则
,则![]() .
.
当![]() 时,由
时,由![]() ,可得
,可得![]() ,
,
由![]() 可得
可得![]() ,
,
![]() 在
在![]() .上单调递增,在
.上单调递增,在![]() 上单调递减.
上单调递减.
故![]()
令![]() ,下证:当
,下证:当![]() 时,
时,![]() .
.
即证![]() ,令
,令![]() ,其中
,其中![]() ,则
,则![]() ,
,
则原式等价于证明:当![]() 时,
时,![]() .
.
由(1)的结论知,显然成立.
综上,当![]() 时,函数
时,函数![]() 为
为![]() 上的单调函数,且单调递减.
上的单调函数,且单调递减.


科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高).现从参赛者中抽取了![]() 人,按年龄分成5组,第一组:
人,按年龄分成5组,第一组: ![]() ,第二组:
,第二组: ![]() ,第三组:
,第三组: ![]() ,第四组:
,第四组: ![]() ,第五组:
,第五组: ![]() ,得到如图所示的频率分布直方图,已知第一组有6人.
,得到如图所示的频率分布直方图,已知第一组有6人.
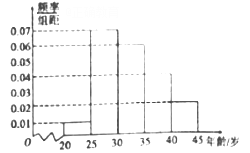
(1)求![]() ;
;
(2)求抽取的![]() 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);
(3)从该市大学生、军人、医务人员、工人、个体户 五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1~5组,从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛,分别代表相应组的成绩,年龄组中1~5组的成绩分别为93,96,97,94,90,职业组中1~5组的成绩分别为93,98,94,95,90.
(Ⅰ)分别求5个年龄组和5个职业组成绩的平均数和方差;
(Ⅱ)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到![]() 的图象
的图象![]() ,只要将
,只要将![]() 图象
图象![]() 怎样变化得到( )
怎样变化得到( )
A.将![]() 的图象
的图象![]() 沿x轴方向向左平移
沿x轴方向向左平移![]() 个单位
个单位
B.将![]() 的图象
的图象![]() 沿x轴方向向右平移
沿x轴方向向右平移![]() 个单位
个单位
C.先作![]() 关于x轴对称图象
关于x轴对称图象![]() ,再将图象
,再将图象![]() 沿x轴方向向右平移
沿x轴方向向右平移![]() 个单位
个单位
D.先作![]() 关于x轴对称图象
关于x轴对称图象![]() ,再将图象
,再将图象![]() 沿x轴方向向左平移
沿x轴方向向左平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵(qian du);阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖膈(bie nao)指四个面均为直角三角形的四面体.如图在堑堵![]() 中,
中,![]() .
.
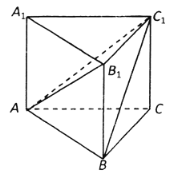
(1)求证:四棱锥![]() 为阳马;
为阳马;
(2)若![]() ,当鳖膈
,当鳖膈![]() 体积最大时,求锐二面角
体积最大时,求锐二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】.(本小题满分16分)
已知函数![]() ,并设
,并设![]() ,
,
(1)若![]() 图像在
图像在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 、
、![]() 的值;
的值;
(2)若函数![]() 是
是![]() 上单调递减,则
上单调递减,则
① 当![]() 时,试判断
时,试判断![]() 与
与![]() 的大小关系,并证明之;
的大小关系,并证明之;
② 对满足题设条件的任意![]() 、
、![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,O为坐标原点,点F为抛物线C1:![]() 的焦点,且抛物线C1上点P处的切线与圆C2:
的焦点,且抛物线C1上点P处的切线与圆C2:![]() 相切于点Q.
相切于点Q.

(Ⅰ)当直线PQ的方程为![]() 时,求 抛物线C1的方程;
时,求 抛物线C1的方程;
(Ⅱ)当正数P变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代科学家祖冲之儿子祖暅在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”(“幂”是截面积,“势”是几何体的高),意思是两个同高的几何体,如在等高处截面的面积恒相等,则它们的体积相等.已知某不规则几何体与如图所示的三视图所表示的几何体满足“幂势既同”,则该不规则几何体的体积为( )
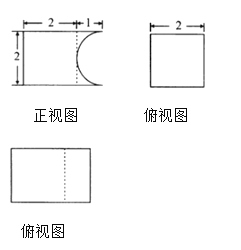
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,试问在
,试问在![]() 轴上是否存在定点
轴上是否存在定点![]() 使得直线
使得直线![]() 与直线
与直线![]() 恰关于
恰关于![]() 轴对称?若存在,求出点
轴对称?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com