
【题目】.(本小题满分16分)
已知函数![]() ,并设
,并设![]() ,
,
(1)若![]() 图像在
图像在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 、
、![]() 的值;
的值;
(2)若函数![]() 是
是![]() 上单调递减,则
上单调递减,则
① 当![]() 时,试判断
时,试判断![]() 与
与![]() 的大小关系,并证明之;
的大小关系,并证明之;
② 对满足题设条件的任意![]() 、
、![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围
的取值范围
【答案】(1)因为![]() ,所以
,所以![]() , …………………2分
, …………………2分
又因为![]() 图像在
图像在![]() 处的切线方程为
处的切线方程为![]() ,
,
所以 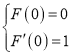 ,即
,即![]() ,解得
,解得 ![]() ,
,![]() . ……………………………………4分
. ……………………………………4分
(2)①因为![]() 是
是![]() 上的单调递减函数,所以
上的单调递减函数,所以![]() 恒成立,
恒成立,
即![]() 对任意的
对任意的![]() 恒成立, ………………………………………6分
恒成立, ………………………………………6分
所以![]() ,所以
,所以![]() ,即
,即![]() 且
且![]() ,
,
令![]() ,由
,由![]() ,知
,知![]() 是减函数,
是减函数,
故![]() 在
在![]() 内取得最小值
内取得最小值![]() ,又
,又![]() ,
,
所以![]() 时,
时,![]() . ……………………………………10分
. ……………………………………10分
② 由①知,![]() ,当
,当![]() 时,
时,![]() 或
或![]() ,
,
因为![]() ,即
,即![]() ,解得
,解得![]() ,
,![]() 或
或![]() ,所以
,所以![]() ,
,
而![]() ,
,
所以![]() 或
或![]() ,
,
不等式![]() 等价于
等价于![]() ,
,
变为![]() 或
或![]() 恒成立,
恒成立,![]() , ………………………………………………12分
, ………………………………………………12分
当![]() 时,
时,![]() ,即
,即![]() ,所以不等式
,所以不等式![]() 恒成立等价于
恒成立等价于![]() 恒成立,等价于
恒成立,等价于![]() , ………………………………………14分
, ………………………………………14分
而 ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以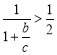 ,
,
所以![]() ,所以
,所以![]() . ……………………………………………………16分
. ……………………………………………………16分
【解析】略


科目:高中数学 来源: 题型:
【题目】某企业引进现代化管理体制,生产效益明显提高.2018年全年总收入与2017年全年总收入相比增长了一倍,实现翻番.同时该企业的各项运营成本也随着收入的变化发生了相应变化.下图给出了该企业这两年不同运营成本占全年总收入的比例,下列说法正确的是( )
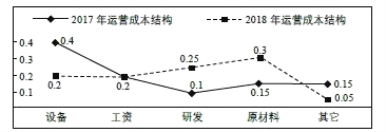
A.该企业2018年原材料费用是2017年工资金额与研发费用的和
B.该企业2018年研发费用是2017年工资金额、原材料费用、其它费用三项的和
C.该企业2018年其它费用是2017年工资金额的![]()
D.该企业2018年设备费用是2017年原材料的费用的两倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选一个,补充在下面问题中的横线上,并解答相应的问题.
这三个条件中任选一个,补充在下面问题中的横线上,并解答相应的问题.
在![]() 中,内角A,B,C的对边分别为a,b,c,且满足________________,
中,内角A,B,C的对边分别为a,b,c,且满足________________,![]()
![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,中华人民共和国成立70周年,为了庆祝建国70周年,某中学在全校进行了一次爱国主义知识竞赛,共1000名学生参加,答对题数(共60题)分布如下表所示:
组别 |
|
|
|
|
|
|
频数 | 10 | 185 | 265 | 400 | 115 | 25 |
答对题数![]() 近似服从正态分布
近似服从正态分布![]() ,
,![]() 为这1000人答对题数的平均值(同一组数据用该组区间的中点值作为代表).
为这1000人答对题数的平均值(同一组数据用该组区间的中点值作为代表).
(1)估计答对题数在![]() 内的人数(精确到整数位).
内的人数(精确到整数位).
(2)学校为此次参加竞赛的学生制定如下奖励方案:每名同学可以获得2次抽奖机会,每次抽奖所得奖品的价值与对应的概率如下表所示.
获得奖品的价值(单位:元) | 0 | 10 | 20 |
概率 |
|
|
|
用![]() (单位:元)表示学生甲参与抽奖所得奖品的价值,求
(单位:元)表示学生甲参与抽奖所得奖品的价值,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,试问在
,试问在![]() 轴上是否存在定点
轴上是否存在定点![]() 使得直线
使得直线![]() 与直线
与直线![]() 恰关于
恰关于![]() 轴对称?若存在,求出点
轴对称?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com