
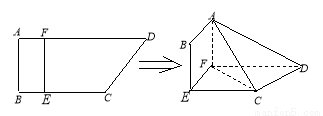
如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=8,BC=6,AB=2,E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使得平面ABEF  平面EFDC.
平面EFDC.
(Ⅰ)当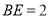 ,是否在折叠后的AD上存在一点
,是否在折叠后的AD上存在一点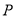 ,且
,且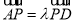 ,使得CP∥平面ABEF?若存在,求出
,使得CP∥平面ABEF?若存在,求出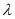 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅱ)设BE=x,问当x为何值时,三棱锥A CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.
(1)存在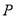 点,
点, ;(2)当
;(2)当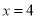 时,三棱锥
时,三棱锥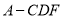 的最大值
的最大值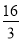 .
.
【解析】
试题分析:(1)与立体几何有关的探索问题:第一步:假设符合条件的结论存在;第二步:从假设出发,利用空间中点、线、面的位置关系求解;第三步,确定符合要求的结论存在或不存在;第四步:给出明确结果;第五步:反思回顾,查看关键点;(2)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;四是利用线面平行的定义,一般用反证法;(3)在求所列函数的最值时,若用基本不等式时,等号取不到时,可利用函数的单调性求解;(4)基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,常常用于比较数的大小或证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好利用基本不等式的切入点.
试题解析:【解析】
(Ⅰ)假设存在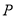 使得满足条件CP∥平面ABEF
使得满足条件CP∥平面ABEF
在平面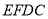 内过点
内过点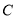 作
作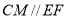 交
交 于
于 ,在平面
,在平面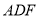 内作直线
内作直线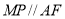 交
交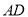 于点
于点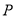 ,连结
,连结 3分
3分
∵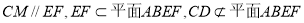
∴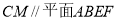 4分
4分
∵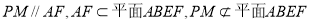
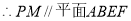 5分
5分
又
∴平面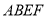 ∥平面
∥平面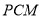 6分
6分
又∵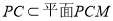
∴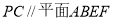 ,故点
,故点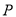 就是所求的点 7分
就是所求的点 7分
又∵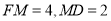
∴ 8分
8分
(Ⅱ)因为平面ABEF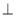 平面EFDC,平面ABEF
平面EFDC,平面ABEF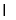 平面EFDC=EF,又AF
平面EFDC=EF,又AF EF,
EF,
所以AF⊥平面EFDC 10分
由已知BE=x,所以AF=x(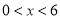 ),则FD=8
),则FD=8 x.
x.
∴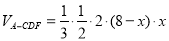 12分
12分
故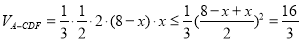
当且仅当 ,即
,即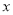 =4时,等号成立
=4时,等号成立
所以,当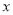 =4时,
=4时,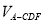 有最大值,最大值为
有最大值,最大值为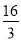 14分
14分
解法二:
故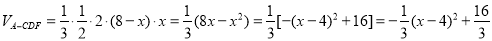
所以,当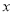 =4时,
=4时,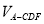 有最大值,最大值为
有最大值,最大值为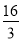 14分
14分
考点:(1)探究性问题;(2)求体积的最大值.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源:2016届福建省高一下学期第一阶段考试数学试卷(解析版) 题型:选择题
平面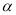 截球O的球面所得圆的半径为1,球心O到平面α的距离为
截球O的球面所得圆的半径为1,球心O到平面α的距离为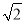 ,则此球的体积为( )
,则此球的体积为( )
A.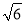 π B.4
π B.4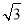 π C.4
π C.4 π D.6
π D.6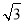 π
π
查看答案和解析>>
科目:高中数学 来源:2016届福建省晋江市高一下学期期末考试数学试卷(解析版) 题型:选择题
若 、
、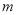 、
、 是互不相同的直线,
是互不相同的直线, 是不重合的平面,则下列命题中为真命题的是( )
是不重合的平面,则下列命题中为真命题的是( )
A.若 ∥
∥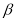 ,
,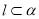 ,
,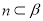 ,则
,则 ∥
∥
B.若 ,则
,则
C.若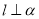 ,
, ∥
∥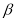 ,则
,则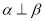
D.若 ,则
,则 ∥
∥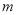
查看答案和解析>>
科目:高中数学 来源:2016届福建省高一第二次质检数学试卷(解析版) 题型:填空题
某校高一年1班参加“唱响校园,放飞梦想”歌咏比赛,得分情况如茎叶图所示,则这组数据的中位数是 。

查看答案和解析>>
科目:高中数学 来源:2016届福建省高一下学期期末考试数学试卷(解析版) 题型:解答题
某地需要修建一条大型输油管道通过240公里宽的沙漠地带,该段输油管道两端的输油站已建好,余下工程是在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为400万元,铺设距离为 公里的相邻两增压站之间的输油管道费用为
公里的相邻两增压站之间的输油管道费用为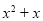 万元.设余下工程的总费用为
万元.设余下工程的总费用为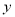 万元.
万元.
(1)试将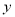 表示成
表示成 的函数;
的函数;
(2)需要修建多少个增压站才能使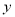 最小,其最小值为多少?
最小,其最小值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com