
【题目】已知函数![]() ,
,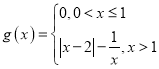 ,则方程
,则方程![]() 的实根个数为( )
的实根个数为( )
A.2个B.3个C.4个D.5个
【答案】C
【解析】
解![]() ,即解
,即解![]() .再分
.再分![]() 与
与![]() ,分别找到函数
,分别找到函数![]() 与
与![]() 在区间
在区间![]() 、
、![]() 、
、![]() 上的单调性,则可找到方程的实数根的个数.
上的单调性,则可找到方程的实数根的个数.
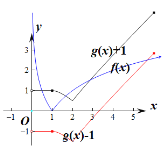
![]()
![]()
1)![]() ,
,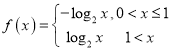 ,
,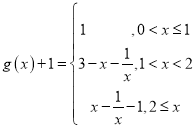 .
.
①当![]() 时,
时,![]() .即
.即![]() 在
在![]() 上有1个零点.
上有1个零点.
②当![]() 时,
时,![]() ,记
,记![]() ,
,
因为 ![]() 在
在![]() 上单调递增,
上单调递增,![]() 在
在![]() 单调递增,
单调递增,
所以![]() 在
在![]() 单调递增,
单调递增,
又![]() ,
,![]() ,由零点存在定理知道
,由零点存在定理知道![]() 在
在![]() 上有唯一零点.
上有唯一零点.
③当![]() 时,
时,![]() ,记
,记![]() ,
,![]() ,记
,记![]() ,开口向下,且
,开口向下,且![]() ,即
,即![]() 恒成立,即
恒成立,即![]() ,即
,即![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,即
,即![]() 在
在![]() 上存在且有唯一零点.
上存在且有唯一零点.
2)![]() ,
,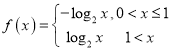 ,
,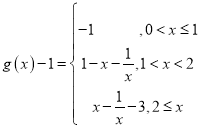 .
.
①当![]() 时,
时,![]() 无解.即
无解.即![]() 在
在![]() 上无零点.
上无零点.
②当![]() 时,
时,![]() ,记
,记![]() ,
,
因为 ![]() 在
在![]() 上单调递增,
上单调递增,![]() 在
在![]() 单调递增,
单调递增,
所以![]() 在
在![]() 单调递增,
单调递增,
又![]() ,
,![]() ,由零点存在定理知道
,由零点存在定理知道![]() 在
在![]() 上无零点.
上无零点.
③当![]() 时,
时,![]() ,记
,记![]() ,
,![]() ,记
,记![]() ,开口向下,且
,开口向下,且![]() ,即
,即![]() 恒成立,即
恒成立,即![]() ,即
,即![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,即
,即![]() 在
在![]() 上存在且有唯一零点.
上存在且有唯一零点.
综上所述:方程![]() 的实根个数为4个.
的实根个数为4个.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:  ,其中
,其中![]() 是仪器的月产量.(注:总收益=总成本+利润)
是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润![]() 表示为月产量
表示为月产量![]() 的函数;
的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 图象如图,
图象如图,![]() 是
是![]() 的导函数,则下列数值排序正确的是( )
的导函数,则下列数值排序正确的是( )

A. ![]()
B. ![]()
C. ![]()
D. ![]()
【答案】C
【解析】结合函数的图像可知过点![]() 的切线的倾斜角最大,过点
的切线的倾斜角最大,过点![]() 的切线的倾斜角最小,又因为点
的切线的倾斜角最小,又因为点![]() 的切线的斜率
的切线的斜率![]() ,点
,点![]() 的切线斜率
的切线斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() ,故
,故![]() ,应选答案C。
,应选答案C。
点睛:本题旨在考查导数的几何意义与函数的单调性等基础知识的综合运用。求解时充分借助题设中所提供的函数图形的直观,数形结合进行解答。先将经过两切点![]() 的直线绕点
的直线绕点![]() 逆时针旋转到与函数的图像相切,再将经过两切点的直线绕点
逆时针旋转到与函数的图像相切,再将经过两切点的直线绕点![]() 顺时针旋转到与函数的图像相切,这个过程很容易发现
顺时针旋转到与函数的图像相切,这个过程很容易发现![]() ,从而将问题化为直观图形的问题来求解。
,从而将问题化为直观图形的问题来求解。
【题型】单选题
【结束】
9
【题目】已知![]() 、
、![]() 为双曲线
为双曲线![]() :
:![]() 的左、右焦点,点
的左、右焦点,点![]() 在
在![]() 上,
上,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:4x-3y+6=0和直线l2:x=-![]() .若拋物线C:y2=2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2.
.若拋物线C:y2=2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2.
(1)求抛物线C的方程;
(2)若以拋物线上任意一点M为切点的直线l与直线l2交于点N,试问在x轴上是否存在定点Q,使Q点在以MN为直径的圆上,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为平面直角坐标系
的顶点为平面直角坐标系![]() 的坐标原点
的坐标原点![]() ,焦点为圆
,焦点为圆![]() 的圆心
的圆心![]() .经过点
.经过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点,
两点,![]() 在第一象限,
在第一象限,![]() 在第四象限.
在第四象限.
(1)求抛物线![]() 的方程;
的方程;
(2)是否存在直线![]() 使
使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为![]() ,
,![]() ,…,
,…,![]() ).
).

(1)求成绩在![]() 的频率,并补全此频率分布直方图;
的频率,并补全此频率分布直方图;
(2)求这次考试平均分的估计值;
(3)若从成绩在![]() 和
和![]() 的学生中任选两人,求他们的成绩在同一分组区间的概率.
的学生中任选两人,求他们的成绩在同一分组区间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为实数,数列
为实数,数列![]() 满足
满足![]() ,
,![]() .
.
(Ⅰ)当![]() 和
和![]() 时,分别写出数列
时,分别写出数列![]() 的前5项;
的前5项;
(Ⅱ)证明:当![]() 时,存在正整数
时,存在正整数![]() ,使得
,使得![]() ;
;
(Ⅲ)当![]() 时,是否存在实数
时,是否存在实数![]() 及正整数
及正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ?若存在,求出实数
?若存在,求出实数![]() 及正整数
及正整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家电公司根据销售区域将销售员分成![]() ,
,![]() 两组.
两组.![]() 年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间
年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间![]() ,
,![]() ,
,![]() ,
,![]() 内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知销售员的年销售额都在区间
内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知销售员的年销售额都在区间![]() 内,将这些数据分成4组:
内,将这些数据分成4组:![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下两个频率分布直方图:
,得到如下两个频率分布直方图:
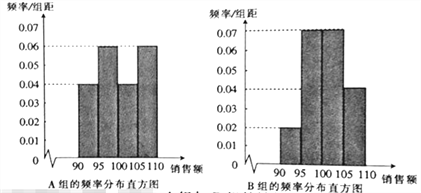
以上面数据的频率作为概率,分别从![]() 组与
组与![]() 组的销售员中随机选取1位,记
组的销售员中随机选取1位,记![]() ,
,![]() 分别表示
分别表示![]() 组与
组与![]() 组被选取的销售员获得的年终奖.
组被选取的销售员获得的年终奖.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)试问![]() 组与
组与![]() 组哪个组销售员获得的年终奖的平均值更高?为什么?
组哪个组销售员获得的年终奖的平均值更高?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com