
【题目】如图,在四棱锥![]() ABCD中,
ABCD中,![]() 和
和![]() 都是等边三角形,平面PAD
都是等边三角形,平面PAD![]() 平面ABCD,且
平面ABCD,且![]() ,
,![]() .
.
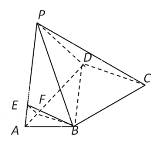
(1)求证:CD![]() PA;
PA;
(2)E,F分别是棱PA,AD上的点,当平面BEF//平面PCD时,求四棱锥![]() 的体积.
的体积.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】数学中有许多形状优美寓意美好的曲线,曲线![]() 就是其中之一(如图).给出下列三个结论:
就是其中之一(如图).给出下列三个结论:

①曲线![]() 恰好经过6个整点(即横纵坐标均为整数的点);
恰好经过6个整点(即横纵坐标均为整数的点);
②曲线![]() 上存在到原点的距离超过
上存在到原点的距离超过![]() 的点;
的点;
③曲线![]() 所围成的“心形”区域的面积小于3.
所围成的“心形”区域的面积小于3.
其中,所有错误结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() ,
,![]() ;
;
(2)函数![]() 图像与
图像与![]() 轴负半轴的交点为
轴负半轴的交点为![]() ,且在点
,且在点![]() 处的切线方程为
处的切线方程为![]() ,函数
,函数![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(3)关于![]() 的方程
的方程![]() 有两个实数根
有两个实数根![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 的短轴长为2,离心率为
的短轴长为2,离心率为![]() .
.
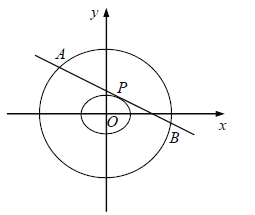
(1)求椭圆E的标准方程;
(2)若直线l与椭圆E相切于点P(点P在第一象限内),与圆![]() 相交于点A,B,且
相交于点A,B,且![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,把满足条件
,把满足条件![]()
![]() 的所有数列
的所有数列![]() 构成的集合记为
构成的集合记为![]() .
.
(1)若数列![]() 的通项为
的通项为![]() ,则
,则![]() 是否属于
是否属于![]() ?
?
(2)若数列![]() 是等差数列,且
是等差数列,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若数列![]() 的各项均为正数,且
的各项均为正数,且![]() ,数列
,数列![]() 中是否存在无穷多项依次成等差数列,若存在,给出一个数列
中是否存在无穷多项依次成等差数列,若存在,给出一个数列![]() 的通项;若不存在,说明理由.
的通项;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
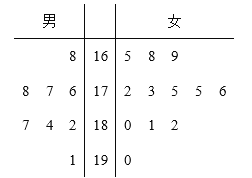
【题目】第30届夏季奥运会将于2012年7月27日在伦敦举行,当地某学校招募了8名男志愿者和12名女志愿者.将这20名志愿者的身高编成如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
(I)如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(Ⅱ)若从所有“高个子”中选3名志愿者,用X表示所选志愿者中能担任“礼仪小姐”的人数,试写出X的分布列,并求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 在椭圆
在椭圆![]() 上,过点
上,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() ,已知点
,已知点![]() 的轨迹是过点
的轨迹是过点![]() 的圆.
的圆.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 在
在![]() 轴的同侧),
轴的同侧),![]() ,
,![]() 为椭圆的左、右焦点,若
为椭圆的左、右焦点,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬我国古代的“六艺文化”,某夏令营主办单位计划利用暑期开设“礼”“乐”“射”“御”“书”“数”六门体验课程,每周一门,连续开设六周.则“课程‘乐’不排在第一周,课程‘御’不排在最后一周”的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com