
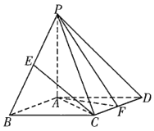
【题目】如图,在四棱锥![]() 中,已知底面
中,已知底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)可先证线线平行,然后根据线面平行的判定定理证明线面平行,也可先根据线线平行证明面面平行,再根据面面平行证明线面平行;
(2)可利用传统法,先找到线在直角三角形求线面角的正弦值,也可根据题中的线面位置关系建立空间直角坐标系,利用空间向量法进行求解.
(1)如图所示,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
因为![]() 是棱
是棱![]() 的中点,所以
的中点,所以![]() 是
是![]() 的中位线,所以
的中位线,所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又由![]() 是棱
是棱![]() 的中点,
的中点,![]() 为
为![]() 的中点,可得
的中点,可得![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又由![]() ,且
,且![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,由
,由![]() 是等边三角形,所以
是等边三角形,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() 两两垂直,故以
两两垂直,故以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,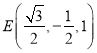 ,
,
故![]() ,
,![]() ,
,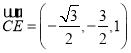 .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则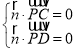 ,即
,即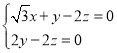 ,
,
令![]() ,则
,则![]() ,故
,故![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则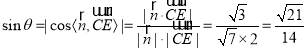 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,现有如下四个结论:
,现有如下四个结论:
![]() ;
;![]() 平面
平面![]() ;
;
![]() 三棱锥
三棱锥![]() 的体积为定值;
的体积为定值;![]() 异面直线
异面直线![]() 所成的角为定值,
所成的角为定值,
其中正确结论的序号是______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() ABCD中,
ABCD中,![]() 和
和![]() 都是等边三角形,平面PAD
都是等边三角形,平面PAD![]() 平面ABCD,且
平面ABCD,且![]() ,
,![]() .
.
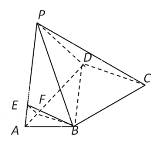
(1)求证:CD![]() PA;
PA;
(2)E,F分别是棱PA,AD上的点,当平面BEF//平面PCD时,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 在椭圆
在椭圆![]() 上,过点
上,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() ,已知点
,已知点![]() 的轨迹是过点
的轨迹是过点![]() 的圆.
的圆.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 在
在![]() 轴的同侧),
轴的同侧),![]() ,
,![]() 为椭圆的左、右焦点,若
为椭圆的左、右焦点,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,![]() 底面ABC,
底面ABC,![]() ,
,![]() ,
,![]() ,D,E分别为棱BC,PC的中点,点F在棱PA上,设
,D,E分别为棱BC,PC的中点,点F在棱PA上,设![]() .
.
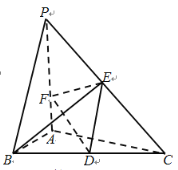
(1)当![]() 时,求异面直线DF与BE所成角的余弦值;
时,求异面直线DF与BE所成角的余弦值;
(2)试确定t的值,使二面角C-EF-D的平面角的余弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国法定劳动年龄是![]() 周岁至退休年龄(退休年龄一般指男
周岁至退休年龄(退休年龄一般指男![]() 周岁,女干部身份
周岁,女干部身份![]() 周岁,女工人
周岁,女工人![]() 周岁).为更好了解我国劳动年龄人口变化情况,有关专家统计了
周岁).为更好了解我国劳动年龄人口变化情况,有关专家统计了![]() 年我国劳动年龄人口和
年我国劳动年龄人口和![]() 周岁人口数量(含预测),得到下表:
周岁人口数量(含预测),得到下表:
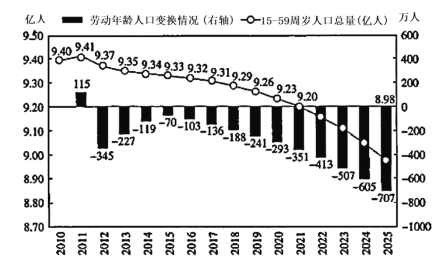
其中![]() 年劳动年龄人口是
年劳动年龄人口是![]() 亿人,则下列结论不正确的是( )
亿人,则下列结论不正确的是( )
A.![]() 年劳动年龄人口比
年劳动年龄人口比![]() 年减少了
年减少了![]() 万人以上
万人以上
B.![]() 这
这![]() 年
年![]() 周岁人口数的平均数是
周岁人口数的平均数是![]() 亿
亿
C.![]() 年,
年,![]() 周岁人口数每年的减少率都小于同年劳动人口每年的减少率
周岁人口数每年的减少率都小于同年劳动人口每年的减少率
D.![]() 年这
年这![]() 年
年![]() 周岁人口数的方差小于这
周岁人口数的方差小于这![]() 年劳动人口数的方差
年劳动人口数的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,斜率为![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,已知点
两点,已知点![]() 的横坐标比点
的横坐标比点![]() 的横坐标大4,直线
的横坐标大4,直线![]() 交线段
交线段![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
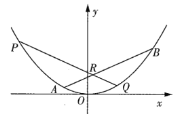
(1)若点![]() 的横坐标等于0,求
的横坐标等于0,求![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了提升学生“数学建模”的核心素养,某校数学兴趣活动小组指导老师给学生布置了一项探究任务:如图,有一张边长为27cm的等边三角形纸片ABC,从中裁出等边三角形纸片![]() 作为底面,从剩余梯形
作为底面,从剩余梯形![]() 中裁出三个全等的矩形作为侧面,围成一个无盖的三棱柱(不计损耗).
中裁出三个全等的矩形作为侧面,围成一个无盖的三棱柱(不计损耗).
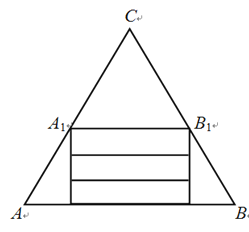
(1)若三棱柱的侧面积等于底面积,求此三棱柱的底面边长;
(2)当三棱柱的底面边长为何值时,三棱柱的体积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com