解:(1)

,则x>1时,f′(x)>0;0<x<1时,f′(x)<0.
所以,函数f(x)在(0,1)上是减函数,在(1,+∞)上是增函数.(2分)
当m≥1时,函数f(x)在[m,m+1]上是增函数,
此时

;
当0<m<1时,函数f(x)在[m,1]上是减函数,在[1,m+1]上是增函数,
此时f(x)
min=f(1)=e;(6分)
(2)证明:
考察函数g(x)=xe
-x,g′(x)=(1-x)e
-x所以g(x)在(-∞,1)内是增函数,在(1,+∞)内是减函数.(结论1)
考察函数F(x)=g(x)-g(2-x),即F(x)=xe
-x+(x-2)e
x-2于是F'(x)=(x-1)(e
2x-2-1)e
-x当x>1时,2x-2>0,从而e
2x-2-1>0,又e
-x>0,所以F′(x)>0,从而函数F(x)在[1,+∞)是增函数.
又F(1)=e
-1-e
-1=0,所以x>1时,有F(x)>F(1)=0,即g(x)>g(2-x).(结论2)(9分)
若(x
1-1)(x
2-1)=0,由结论1及g(x
1)=g(x
2),得x
1=x
2=1,与x
1≠x
2矛盾;
若(x
1-1)(x
2-1)>0,由结论1及g(x
1)=g(x
2),得x
1=x
2,与x
1≠x
2矛盾;(11分)
若(x
1-1)(x
2-1)<0,不妨设x
1<1,x
2>1
由结论2可知,g(x
2)>g(2-x
2),所以g(x
1)=g(x
2)>g(2-x
2).
因为x
2>1,所以2-x
2<1,又由结论1可知函数g(x)在区间(-∞,1)内是增函数,
所以x
1>2-x
2,即x
1+x
2>2.(15分)
分析:(1)先求其导函数,找到其增减区间即可求函数f(x)在[m,m+1](m>0)上的最小值;
(2)先求出函数g(x)的增减区间,再利用题中要证的结论构造新函数F(x)=g(x)-g(2-x),求出新函数F(x)=g(x)-g(2-x)的增减区间,把二者相结合即可证明结论.
点评:本题的第一问主要考查利用导函数求函数在闭区间上的最值问题,比较基础,第二问就比较难,适合中上等学生来做.

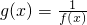 ,如果x1≠x2,且g(x1)=g(x2),证明:x1+x2>2.
,如果x1≠x2,且g(x1)=g(x2),证明:x1+x2>2. ,则x>1时,f′(x)>0;0<x<1时,f′(x)<0.
,则x>1时,f′(x)>0;0<x<1时,f′(x)<0. ;
;

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案