(1)解:由题意a>0,f′(x)=e
x-a,
由f′(x)=e
x-a=0得x=lna.
当x∈(-∞,lna)时,f′(x)<0;当x∈(lna,+∞)时,f′(x)>0.
∴f(x)在(-∞,lna)单调递减,在(lna,+∞)单调递增.
即f(x)在x=lna处取得极小值,且为最小值,其最小值为f(lna)=e
lna-alna-1=a-alna-1.(5分)
(2)解:f(x)≥0对任意的x∈R恒成立,即在x∈R上,f(x)
min≥0.
由(1),设g(a)=a-alna-1,所以g(a)≥0.
由g′(a)=1-lna-1=-lna=0得a=1.
∴g(a)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,
∴g(a)在a=1处取得最大值,而g(1)=0.
因此g(a)≥0的解为a=1,∴a=1.(9分)
(3)证明:由(2)知,对任意实数x均有e
x-x-1≥0,即1+x≤e
x.
令
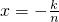
(n∈N
*,k=0,1,2,3,…,n-1),则
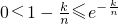
.
∴
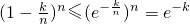
.
∴
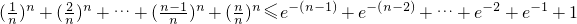
=
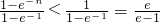
.(14分)
分析:(1)求导函数,确定函数的单调性,从而可得f(x)在x=lna处取得极小值,且为最小值;
(2)f(x)≥0对任意的x∈R恒成立,即在x∈R上,f(x)
min≥0.由(1),构造函数g(a)=a-alna-1,所以g(a)≥0,确定函数的单调性,即可求得实数a的值;
(3)由(2)知,对任意实数x均有e
x-x-1≥0,即1+x≤e
x,令
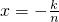
(n∈N
*,k=0,1,2,3,…,n-1),可得
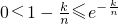
,从而有
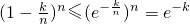
,由此即可证得结论.
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查恒成立问题,同时考查不等式的证明,解题的关键是正确求导数,确定函数的单调性.

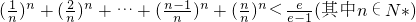 .
.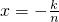 (n∈N*,k=0,1,2,3,…,n-1),则
(n∈N*,k=0,1,2,3,…,n-1),则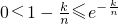 .
.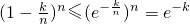 .
.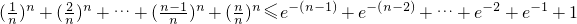
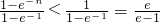 .(14分)
.(14分)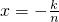 (n∈N*,k=0,1,2,3,…,n-1),可得
(n∈N*,k=0,1,2,3,…,n-1),可得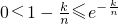 ,从而有
,从而有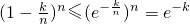 ,由此即可证得结论.
,由此即可证得结论.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案