
分析 (1)由题意可得c=2,即可求出b=2,即可求出椭圆的标准方程,
(2)设A(2$\sqrt{2}$cosα,2sinα),B(2$\sqrt{2}$cosβ,2sinβ),根据题意和点P在椭圆上,化简整理可得a-β=$\frac{π}{2}$,再根据中点坐标公式,消α,线段AB中点Q的轨迹为E的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1,再设M,N两点的坐标为(x1,y1),(x2,y2),根据弦长公式即可求出.
解答 解:(1)∵点F1,F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
∴2c=4,b=2,
故c=2,a=2$\sqrt{2}$,
故椭圆C的标准方程为:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$;
(2)设A(2$\sqrt{2}$cosα,2sinα),B(2$\sqrt{2}$cosβ,2sinβ),
∵$\overrightarrow{OP}$=$\frac{3}{5}$$\overrightarrow{OA}$+$\frac{4}{5}$$\overrightarrow{OB}$,
∴$\overrightarrow{OP}$=($\frac{6\sqrt{2}cosα+8\sqrt{2}cosβ}{5}$,$\frac{6sinα+8sinβ}{5}$),
∵点P在椭圆上,
∴(3cosα+4cosβ)2+(3sinα+4sinβ)2=25,
∴cosαcosβ+sinαsinβ=0,
∴cos(α-β)=0,
∴a-β=$\frac{π}{2}$,
∴B(2$\sqrt{2}$sinα,-2cosα),
∴AB中点Q的坐标为($\sqrt{2}$cosα+$\sqrt{2}$sinα,sinα-cosα),
设Q的点坐标为(x,y),
∴x=$\sqrt{2}$cosα+$\sqrt{2}$sinα,y=sinα-cosα,
∴$\frac{{x}^{2}}{4}$=cos2α+2cosαsinα+sin2α=1+2cosαsinα,y2=cos2α-2cosαsinα+sin2α=1-2cosαsinα
∴$\frac{{x}^{2}}{4}$+y2=2,
即线段AB中点Q的轨迹为E的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1,
设M,N两点的坐标为(x1,y1),(x2,y2),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1}\\{y=x+1}\end{array}\right.$,消y,整理得5x2+8x-4=0,
∴x1+x2=-$\frac{8}{5}$,x1x2=-$\frac{4}{5}$,
∴|MN|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{1+1}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}$•$\sqrt{\frac{64}{25}+\frac{16}{5}}$=$\frac{12\sqrt{2}}{5}$.
点评 本题考查了椭圆的方程,弦长公式,以及点的轨迹方程,关键是巧设点的坐标,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | y=-2x+3 | B. | y=x | C. | y=3x-2 | D. | y=2x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
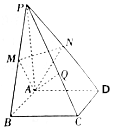 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠ABC=60°,PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点.
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠ABC=60°,PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
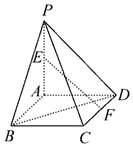 如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F分别是线段PA,CD的中点,则异面直线EF与BD所成角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F分别是线段PA,CD的中点,则异面直线EF与BD所成角的余弦值为$\frac{\sqrt{3}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
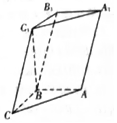 如图所示,三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°.
如图所示,三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com