
���� ��1����������ɵã�a=$\frac{1}{3}$���ٸ��ݵȱ����е����ʼ������c��
��2�����������{an}��ͨ�ʽ���ٸ�������ɵ�$\sqrt{{S}_{n}}$-$\sqrt{{S}_{n-1}}$=1���������֤�����ٸ������еĵ��ƹ�ʽ���bn��
��3������������ͣ������������$\left\{{\frac{1}{{{b_n}{b_{n+1}}}}}\right\}$ǰn���ΪTn���ٷ����������m�ķ�Χ��
��� �⣺��1����f��1��=$\frac{1}{3}$��
��a=$\frac{1}{3}$��
��f��x��=��$\frac{1}{3}$��x��
��a1=f��1��-c=$\frac{1}{3}$-c
��a2=[f��2��-c]-[f��1��-c]=-$\frac{2}{9}$��
a3=[f��3��-c]-[f��2��-c]=-$\frac{2}{27}$��
������{an}�ɵȱ����У�
��a1a3=a22��
����$\frac{1}{3}$-c��•��-$\frac{2}{27}$��=��-$\frac{2}{9}$��2��
��c=1��
��2��֤�����߹���q=$\frac{{a}_{2}}{{a}_{1}}$=$\frac{1}{3}$��
��an=-$\frac{2}{3}$��$\frac{1}{3}$��n-1=-2��$\frac{1}{3}$��n��
��Sn-Sn-1=��$\sqrt{{S}_{n}}$-$\sqrt{{S}_{n-1}}$����$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$��=��$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$����
��bn��0��$\sqrt{{S}_{n}}$��0��
��$\sqrt{{S}_{n}}$-$\sqrt{{S}_{n-1}}$=1��
������{$\sqrt{{S}_{n}}$}����һ������Ϊ1����Ϊ1�ĵȲ����У�
��$\sqrt{{S}_{n}}$=1+��n-1����1=n��
��Sn=n2��
��n��2ʱ��
��bn=Sn-Sn-1=n2-��n-1��2=2n-1��
��n=1ʱ��b1=1��������ʽ��
��bn=2n-1��n��N*��
��$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{��2n-1����2n+1��}$=$\frac{1}{2}$��$\frac{1}{2n-1}$-$\frac{1}{2n+1}$����
��Tn=$\frac{1}{1��3}$+$\frac{1}{3��5}$+$\frac{1}{5��7}$+��+$\frac{1}{��2n-1����2n+1��}$
=$\frac{1}{2}$��1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+��+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$��=$\frac{1}{2}$��1-$\frac{1}{2n+1}$����$\frac{1}{3}$��
�߶��������n��N*����Tn��m��
��m��$\frac{1}{3}$��
��m��ȡֵ��ΧΪ��-�ޣ�$\frac{1}{3}$]��
���� ���⿼���˵Ȳ����к͵ȱ����������Լ����������еĹ�ϵ������������ͺͷ������������е��⣮


 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 16�� | B�� | 8�� | C�� | 4�� | D�� | 2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
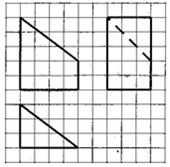
| A�� | 12 | B�� | 18 | C�� | 24 | D�� | 30 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com