Question

在直角坐标平面中，△ABC的两个顶点A，B的坐标分别为A(a,0),B(a,0)(a＞0),两动点M,N满足++=0,||=7||=7||，向量与共线.

（1）求△ABC的顶点C的轨迹；

（2）若过点P(0,a)的直线与点C的轨迹相交于E、F两点，求·的取值范围；

（3）若G(-a,0),H(2a,0),Q点为C点轨迹在第一象限内的任意一点，则是否存在常数λ（λ＞0），使得∠QHG=λ∠QGH恒成立？若存在，求出λ的值；若不存在，请说明理由.

Answer 1

解：（1）设C点的坐标为（x,y）,

∵++=0，

∴M点是△ABC的重心，故可得M为(,).

又||=||且向量与共线，

∴N在边AB的中垂线上.∴N（0,）.

而||=||，∴=·,

即x²=a²，即C点的轨迹是以（-2a,0）,(2a,0)为焦点，实轴长为2a的双曲线.

（2）设E（x₁,y₁）,F(x₂,y₂),过点P（0,a）的直线方程为y=kx+a,代入x²=a²得(3-k²)x²-2akx-4a²=0.①

∴Δ=4a²k²+16a²(3-k²)＞0,k²＜4.

∴k²-3＜1.

∴＞4或＜0.

而x₁,x₂是方程①的两根，

∴x₁+x₂=,x₁x₂=.

∴·=(x₁,y₁-a)·(x₂,y₂-a)=x₁x₂+kx₁·kx₂

=(1+k₂)x₁x₂=

=4a²(1+)∈(-∞,4a²)∪(20a²,+∞).

故·的取值范围为（-∞,4a²)∪(20a²,+∞).

（3）设Q（x₀,y₀）(x₀＞0,y₀＞0),则x₀²=a²，即y₀²=3(x₀²-a²).

当QH⊥x轴时，x₀=2a,y₀=3a,∴∠QGH=,即∠QHG=2∠QGH,故猜想存在λ=2,使∠QHG=λ∠QGH总成立.

当QH不垂直x轴时，tan∠QHG=,tan∠QGH=,

∴tan2∠QGH=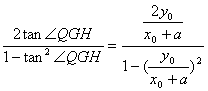

===-=tan∠QHG.

又∵2∠QGH与∠QHG同在（0，）∪(,π)内，

∴2∠QGH=∠QHG.

故存在λ=2,使2∠QGH=∠QHG恒成立.