
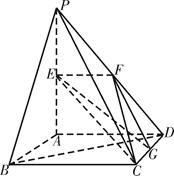
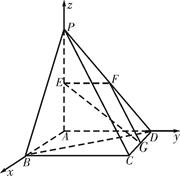
 如图,平面
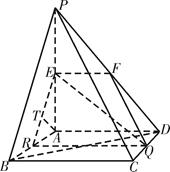
如图,平面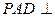 平面ABCD,
平面ABCD,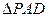 是直角三角形,
是直角三角形, ,E、F、G分别是
,E、F、G分别是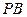 ∥面EFC;
∥面EFC;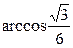 (3)点A到面EFQ的距离为0.8
(3)点A到面EFQ的距离为0.8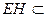 面EFG,PB
面EFG,PB 面EFG,∴PB∥面EFG.
面EFG,∴PB∥面EFG.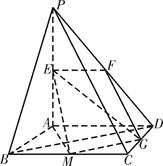 在Rt△MAE中,
在Rt△MAE中,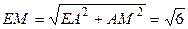 ,
,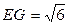 ,又
,又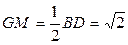 ,
, ,
,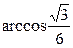 .
. 题设条件. 过点Q作QR⊥AB于R,连结RE,
题设条件. 过点Q作QR⊥AB于R,连结RE, PA=A,∴AD⊥面PAB.
PA=A,∴AD⊥面PAB.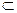 面EFQ,∴面EFQ⊥面PAB.
面EFQ,∴面EFQ⊥面PAB.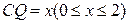 ,则BR=CQ=x,AR=2-x,AE=1,
,则BR=CQ=x,AR=2-x,AE=1,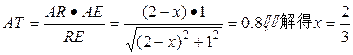 .
. 故存在点Q,当
故存在点Q,当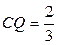 时,点A到面EFQ的距离为0.8.
时,点A到面EFQ的距离为0.8.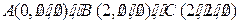 ,
, ,
, .
.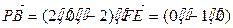 ,
,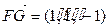 ,
,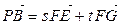 ,即
,即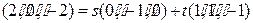 ,
,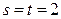 .∴
.∴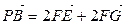 ,又∵
,又∵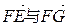 不共线,
不共线,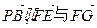 共面. ∵PB
共面. ∵PB 面EFG,∴PB∥面EFG.
面EFG,∴PB∥面EFG.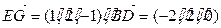 ,
, .故异面直线EG与BD所成的角为
.故异面直线EG与BD所成的角为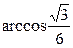
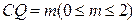 ,则DQ=2-m,
,则DQ=2-m,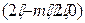 ,∴
,∴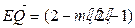 . 而
. 而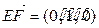 ,设平面EFQ的法向量为n=(x,y,z),则
,设平面EFQ的法向量为n=(x,y,z),则 ,
,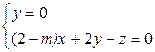 . 令x=1,则
. 令x=1,则 .
.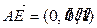 ,∴点A到面EFQ的距离
,∴点A到面EFQ的距离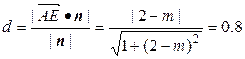 ,
,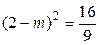 ,∴
,∴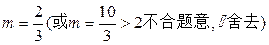 .
.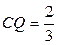 时,点A到面EFQ的距离为0.8.
时,点A到面EFQ的距离为0.8.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源:不详 题型:单选题
 .条件“直线l与平面
.条件“直线l与平面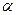 内两条相交直线都垂直”
内两条相交直线都垂直”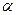 垂直”的( )
垂直”的( )| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.充分非必要条件; | B.必要非充分条件; | C.充要条件; | D.非充分非必要条件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
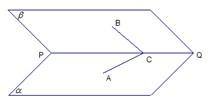
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com