
分析 (1)设h(x)=f(x)-g(x)化为分段函数,由h(x)的图象可知不等式的解集.
(2)转化f(x)≤g(x)为a+1≤x+2,然后求解a的范围.
解答 解:(1)设h(x)=f(x)-g(x)=$\left\{\begin{array}{l}{-5x-2(x≤-\frac{1}{2})}\\{-x(-\frac{1}{2}<x<\frac{1}{2})}\\{3x-2(x≥\frac{1}{2})}\end{array}\right.$
则由h(x)的图象可知不等式的解集{x|x≤0或x≥$\frac{2}{3}$}
(2)当x∈(-$\frac{1}{2}$,$\frac{a}{2}$)时f(x)=a+1,
又f(x)≤g(x),即a+1≤x+2,即x≥a-1恒成立,
a-1≤-$\frac{1}{2}$,∴a≤$\frac{1}{2}$
又∵a>0,∴0<a$≤\frac{1}{2}$
点评 本题考查函数的恒成立,绝对值函数以及分段函数的应用,考查转化思想以及计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{3}$,$\frac{1}{3}$] | B. | [-$\frac{1}{2}$,$\frac{1}{2}$] | C. | [-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$] | D. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
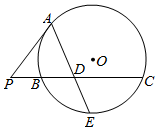 如图,切线PA切圆O于点A,割线PBC与圆O交于点B,C,且PC=2PA,D为线段PC的中点,AD的延长线交圆O于点E.若PB=$\frac{3}{4}$,则AD•DE的值为$\frac{9}{8}$.
如图,切线PA切圆O于点A,割线PBC与圆O交于点B,C,且PC=2PA,D为线段PC的中点,AD的延长线交圆O于点E.若PB=$\frac{3}{4}$,则AD•DE的值为$\frac{9}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在复平面内,复数z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$.设复数z=$\frac{{z}_{1}}{{z}_{2}}$,若a-z为纯虚数,则实数a的值为( )
如图,在复平面内,复数z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$.设复数z=$\frac{{z}_{1}}{{z}_{2}}$,若a-z为纯虚数,则实数a的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com