
���� ��1������������������¼����ʳ˷���ʽ�Ͷ����¼����ʼ��㹫ʽ�г������飬�����a��b��ֵ��
��2�������⣬����Ŷӻ�ý������Ϊ�������X����X��ֵ����Ϊ0��2��4��6��8��10���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�E��X����
��� �⣺��1���������$\left\{\begin{array}{l}{\frac{1}{4}ab=\frac{1}{24}}\\{1-��1-a����1-\frac{1}{4}����1-b��=\frac{3}{4}}\end{array}\right.$��
��a��b�����a=$\frac{1}{2}$��b=$\frac{1}{3}$��
��2�������⣬����Ŷӻ�ý������Ϊ�������X����X��ֵ����Ϊ0��2��4��6��8��10��12��
P��X=0��=$\frac{1}{2}��\frac{2}{3}��\frac{3}{4}=\frac{1}{4}$��
P��X=2��=$\frac{1}{2}��\frac{2}{3}��\frac{3}{4}$=$\frac{1}{4}$��
P��X=4��=$\frac{1}{2}��\frac{1}{3}��\frac{3}{4}$=$\frac{1}{8}$��
P��X=6��=$\frac{1}{2}��\frac{2}{3}��\frac{1}{4}+\frac{1}{2}��\frac{1}{3}��\frac{3}{4}$=$\frac{5}{24}$��
P��X=8��=$\frac{1}{2}��\frac{2}{3}��\frac{1}{4}$=$\frac{1}{12}$��
P��X=10��=$\frac{1}{2}��\frac{1}{3}��\frac{1}{4}$=$\frac{1}{24}$��
P��X=12��=$\frac{1}{2}��\frac{1}{3}��\frac{1}{4}$=$\frac{1}{24}$��
��X�ķֲ���Ϊ��
| X | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| P | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{8}$ | $\frac{5}{24}$ | $\frac{1}{12}$ | $\frac{1}{24}$ | $\frac{1}{24}$ |
���� ���⿼��������¼�����ɢ����������ֲ����������Ȼ���֪ʶ�����ڿ���ѧ����������������������������ȡ������Ϣ���������Լ�����˼�����������˼���Ӧ�ã�


 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
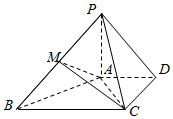 ������P-ABCD�У�AD��BC��DC��AD��PA��ƽ��ABCD��2AD=BC=2$\sqrt{3}$����DAC=30�㣬MΪPB�е㣮
������P-ABCD�У�AD��BC��DC��AD��PA��ƽ��ABCD��2AD=BC=2$\sqrt{3}$����DAC=30�㣬MΪPB�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCD��BDEF��Ϊ���Σ�����DAB=��DBF=60�㣬��FA=FC��
��ͼ���ı���ABCD��BDEF��Ϊ���Σ�����DAB=��DBF=60�㣬��FA=FC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | $\frac{1}{4}$ | C�� | 8 | D�� | $\frac{1}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
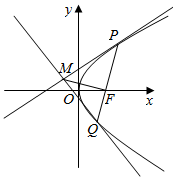 ��ͼ��ʾ��ֱ��l����������y2=2px��p��0���Ľ���F�����������߽��ڵ�P��Q���㣬��P��Q�ֱ��������ߵ����߽���M�����|PF|=a��|QF|=b����|MF|��ֵΪ��������
��ͼ��ʾ��ֱ��l����������y2=2px��p��0���Ľ���F�����������߽��ڵ�P��Q���㣬��P��Q�ֱ��������ߵ����߽���M�����|PF|=a��|QF|=b����|MF|��ֵΪ��������| A�� | a+b | B�� | $\frac{1}{2}��a+b��$ | C�� | ab | D�� | $\sqrt{ab}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com