
分析 (I)利用已知条件得到||x-1|-2|<1,通过去掉绝对值符号,转化求解不等式的解集即可.
(Ⅱ)已知条件转化为:只需要g(x)max≥f(x)min,求出f(x))的最小值,g(x)的最大值,即可求解实数a的取值范围.
解答 解:(I)由|g(x)|<1得:||x-1|-2|<1,
∴-1<|x-1|-2<1,即1<|x-1|<3,
由1<|x-1|解得:x>2或x<0;由|x-1|<3解得:-2<x<4;
∴原不等式的解为(-2,0)∪(2,4).…(5分)
(Ⅱ)因为?x1∈R,x2∈R,使得f(x1)≤g(x2)成立,
只需要g(x)max≥f(x)min
∵f(x)=|2x-a|+|2x+1|≥|(2x-a)-(2x+1)|=|a+1|,g(x)=2-|x-1|≤2,
∴|a+1|≤2,解得-3≤a≤1,
所以实数a的取值范围为{a|-3≤a≤1}.…(10分)
点评 本题考查函数与方程的应用,函数的最值的求法恒成立问题以及绝对值不等式的解法,考查转化思想以及计算能力.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f′(a)<0,f′(b)<0 | B. | f′(a)>0,f′(b)>0 | C. | f′(a)<0,f′(b)>0 | D. | f′(a)>0,f′(b)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
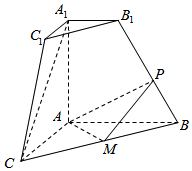 如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2.直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.M为线段BC的中点,P为线段BB1上的动点.
如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2.直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.M为线段BC的中点,P为线段BB1上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com