
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
分析 设双曲线的焦点F(c,0),直线l:x=c,P(c,n),A(-a,0),B(a,0),由两直线的夹角公式可tan∠APB=|$\frac{{k}_{PA}-{k}_{PB}}{1+{k}_{PA}•{k}_{PB}}$|,由直线的斜率公式,化简整理,运用基本不等式,结合离心率公式,即可得到所求最大值.
解答 解:设双曲线的焦点F(c,0),直线l:x=c,
可设点P(c,n),A(-a,0),B(a,0),
由两直线的夹角公式可得tan∠APB=|$\frac{{k}_{PA}-{k}_{PB}}{1+{k}_{PA}•{k}_{PB}}$|
=|$\frac{\frac{n}{c+a}-\frac{n}{c-a}}{1+\frac{{n}^{2}}{{c}^{2}-{a}^{2}}}$|=$\frac{2a|n|}{{n}^{2}+({c}^{2}-{a}^{2})}$=$\frac{2a}{|n|+\frac{{c}^{2}-{a}^{2}}{|n|}}$=tan60°=$\sqrt{3}$,
由|n|+$\frac{{c}^{2}-{a}^{2}}{|n|}$≥2$\sqrt{|n|•\frac{{c}^{2}-{a}^{2}}{|n|}}$=2$\sqrt{{c}^{2}-{a}^{2}}$,
可得$\sqrt{3}$≤$\frac{a}{\sqrt{{c}^{2}-{a}^{2}}}$,
化简可得3c2≤4a2,即c≤$\frac{2\sqrt{3}}{3}$a,
即有e=$\frac{c}{a}$≤$\frac{2\sqrt{3}}{3}$.
当且仅当n=±$\sqrt{{c}^{2}-{a}^{2}}$,即P(c,±$\sqrt{{c}^{2}-{a}^{2}}$),离心率取得最大值$\frac{2\sqrt{3}}{3}$.
故选:A.
点评 本题考查双曲线的离心率的最值的求法,注意运用两直线的夹角公式和直线的斜率公式及基本不等式,考查化简整理的运算能力,属于中档题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,-2) | B. | (0,2) | C. | (0,-1) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
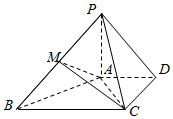 在四棱锥P-ABCD中,AD∥BC,DC⊥AD,PA⊥平面ABCD,2AD=BC=2$\sqrt{3}$,∠DAC=30°,M为PB中点.
在四棱锥P-ABCD中,AD∥BC,DC⊥AD,PA⊥平面ABCD,2AD=BC=2$\sqrt{3}$,∠DAC=30°,M为PB中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com