已知函数f(x)=x|x-a|.
(1)若a=-2,写出函数y=f(x)的单调减区间;
(2)若a=1,函数y=f(x)-m有两个零点,求实数m的值;
(3)若-2≤x≤1时,-2≤f(x)≤4恒成立,求实数a的取值范围.
解:(1)当a=-2时f(x)=
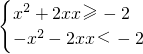
故函数y=f(x)的单调减区间为[-2,-1]
(2)当a=1时f(x)=

在直角坐标系中做出f(x)的图象(如下图)
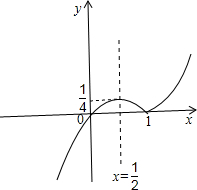
要使函数y=f(x)-m有两个零点即使f(x)-m=0有两个不同的实根即y=f(x)与y=m有两个不同的交点
故m=0或

(3)当0≤x≤1时则f(x)≥0恒成立故要使-2≤x≤1时,-2≤f(x)≤4恒成立须有f(x)
max≤4即
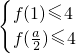
∴0≤a≤4
当-2≤x<0时则f(x)<0恒成立故要使-2≤x≤1时,-2≤f(x)≤4恒成立须有f(x)
min≥-2即
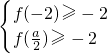
∴
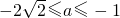
综上:0≤a≤4或
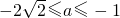
分析:(1)利用绝对值的意义可得当a=-2时f(x)=
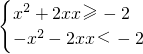
再利用一元二次函数的单调性即可写出递减区间.
(2)根据零点的定义可得要使函数y=f(x)-m有两个零点即使f(x)-m=0有两个不同的实根即y=f(x)与y=m有两个不同的交点因此需做出f(x)的图象再利用数形结合的思想求解.
(3)由于f(x)的正负取决于x故可分0≤x≤1,-2≤x<0两种情况,然后再结合一元二次函数的性质求出f(x)的最大最小值再令f(x)
max≤4且f(x)
min≥-2求出a的范围.
点评:本题主要考查了函数单调性,零点的概念,以及恒成立的问题.解题的关键是第一问要根据绝对值的意义简化f(x)再利用一元二次函数的单调性求解.第二问要将a=1,函数y=f(x)-m有两个零点转化为y=f(x)与y=m有两个不同的交点然后利用数形结合的思想求解.而第三问要分析出-2≤x≤1时,-2≤f(x)≤4恒成立即f(x)
max≤4且f(x)
min≥-2而再求最大最小值时要利用一元二次函数的性质得出当0≤x≤1时f(x)的最大值要么在

要么在1取得,当-2≤x<0时则f(x)的最小值要么在

要么在-2取得!

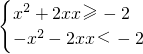 故函数y=f(x)的单调减区间为[-2,-1]
故函数y=f(x)的单调减区间为[-2,-1] 在直角坐标系中做出f(x)的图象(如下图)
在直角坐标系中做出f(x)的图象(如下图)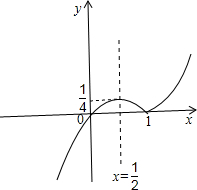

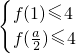
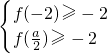
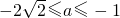
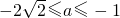
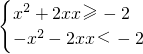 再利用一元二次函数的单调性即可写出递减区间.
再利用一元二次函数的单调性即可写出递减区间. 要么在1取得,当-2≤x<0时则f(x)的最小值要么在
要么在1取得,当-2≤x<0时则f(x)的最小值要么在 要么在-2取得!
要么在-2取得! 

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<