解:(1)由于a
n+1+a
n=4n-56,(n∈N*),
∴a
n+2+a
n+1=4n-52,
∴a
n+2-a
n=4.
∴{a
n}的奇数项与偶数项分别是公差为4的等差数列.
又a
1=a,
∴a
2=-52-a,
∴
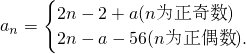
------(4分)
(2)
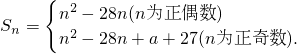
------(6分)
当n=14时,n
2-28n取到最小值为-196,
当n=13或15时,n
2-28n+a+27取到最小值为-168+a,----(8分)
∵
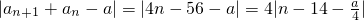
,
当-2≤a≤2时,n=14取到最小值.
∴-168+a≥-196,
即a≥-28
∴-2≤a≤2
当-6≤a<-2或2<a≤6时,n=13或15取到最小值.
∴-168+a≤-196,即a≤-28
∴a不存在------(10分)
综上,存在这样的实数a,取值范围为-2≤a≤2--(12分)
(3)由已知b
2n+1=b
2n+
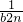
+2,即b
2n+1-b
2n=
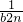
+2
由累差迭加得b
2100-b
21=(
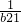
+
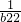
+…+
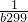
)+198>198
∴b
100>14 (14分)
显然{b
n}递增,b
1=a
15=1,b
2=2,当n>2时,b
n>2,
∴b
2100-b
21=
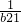
+(
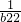
+…+
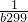
)+198<1+
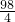
+198<224
∴b
100<15 (16分)
∴b
100的整数部分为14 (18分)
分析:(1)再写一式,两式相减可知∴{a
n}的奇数项与偶数项分别是公差为4的等差数列. 从而分段可写出数列{a
n}的通项公式.
(2)分段求前n项和为S
n,再求S
n与|a
n+1+a
n-a|同时取到最小值,从而可解;
(3)由已知b
2n+1=b
2n+
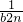
+2,即b
2n+1-b
2n=
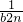
+2,由累差迭加得b
2100-b
21=(
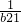
+
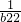
+…+
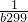
)+198>198,从而可确定b
100的整数部分.
点评:本题以数列递推式为载体,考查数列的通项,考查数列的和,有较强的综合性.

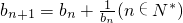 ,求b100的整数部分.
,求b100的整数部分.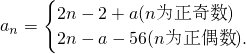 ------(4分)
------(4分)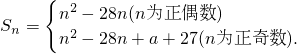 ------(6分)
------(6分)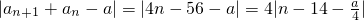 ,
,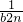 +2,即b2n+1-b2n=
+2,即b2n+1-b2n=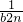 +2
+2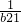 +
+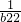 +…+
+…+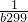 )+198>198
)+198>198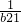 +(
+(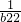 +…+
+…+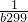 )+198<1+
)+198<1+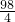 +198<224
+198<224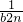 +2,即b2n+1-b2n=
+2,即b2n+1-b2n=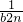 +2,由累差迭加得b2100-b21=(
+2,由累差迭加得b2100-b21=(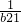 +
+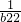 +…+
+…+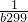 )+198>198,从而可确定b100的整数部分.
)+198>198,从而可确定b100的整数部分.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案