
【题目】设x,y,z为非零实数,满足xy+yz+zx=1,证明:![]() .
.
【答案】不等式的证明一般可以考虑运用作差法或者是利用分析法来证明。
【解析】
试题为使所证式有意义,![]() 三数中至多有一个为0;据对称性,不妨设
三数中至多有一个为0;据对称性,不妨设![]() ,则
,则![]() ;
;
![]() 、当
、当![]() 时,条件式成为
时,条件式成为![]() ,
,![]() ,
,![]() ,而
,而
![]() ,
,
只要证,![]() ,即
,即![]() ,也即
,也即![]() ,此为显然;取等号当且仅当
,此为显然;取等号当且仅当![]() .
.
![]() 、再证,对所有满足
、再证,对所有满足![]() 的非负实数
的非负实数![]() ,皆有
,皆有
![]() .显然,三数
.显然,三数![]() 中至多有一个为0,据对称性,
中至多有一个为0,据对称性,
仍设![]() ,则
,则![]() ,令
,令![]() ,
,![]() 为锐角,以
为锐角,以![]() 为内角,构作
为内角,构作![]() ,则
,则![]()
![]() ,于是
,于是![]() ,且由
,且由![]() 知,
知,![]() ;于是
;于是![]() ,即
,即![]() 是一个非钝角三角形.
是一个非钝角三角形.
下面采用调整法,对于任一个以![]() 为最大角的非钝角三角形
为最大角的非钝角三角形![]() ,固定最大角
,固定最大角![]() ,将
,将![]() 调整为以
调整为以![]() 为顶角的等腰
为顶角的等腰![]() ,其中
,其中![]() ,且设
,且设![]() ,记
,记![]() ,据
,据![]() 知,
知,
![]() .今证明,
.今证明,![]() .即
.即![]()
……①.
即要证![]() ……②
……②
先证![]() ……③,即证
……③,即证![]() ,
,
即 ,此即
,此即![]() ,也即
,也即
![]() ,即
,即![]() ,此为显然.
,此为显然.
由于在![]() 中,
中,![]() ,则
,则![]() ;而在
;而在![]() 中,
中,
![]() ,因此②式成为
,因此②式成为
![]() ……④,
……④,
只要证,![]() ……⑤,即证
……⑤,即证![]() ,注意③式以及
,注意③式以及
![]() ,只要证
,只要证![]() ,即
,即![]() ,也即
,也即![]() …⑥
…⑥
由于最大角![]() 满足:
满足:![]() ,而
,而![]() ,则
,则![]() ,所以
,所以
![]() ,故⑥成立,因此⑤得证,由③及⑤得④成立,从而①成立,即
,故⑥成立,因此⑤得证,由③及⑤得④成立,从而①成立,即![]() ,因此本题得证.
,因此本题得证.


科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 相邻两对称轴间的距离为
相邻两对称轴间的距离为![]() ,若将
,若将![]() 的图象先向左平移
的图象先向左平移![]() 个单位,再向下平移1个单位,所得的函数
个单位,再向下平移1个单位,所得的函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式,并求
的解析式,并求![]() 的对称中心;
的对称中心;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实根,求实数
上有两个不相等的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题16分)某乡镇为了进行美丽乡村建设,规划在长为10千米的河流OC的一侧建一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数![]() ,
,![]() (单位:千米)的图象,且曲线段的顶点为
(单位:千米)的图象,且曲线段的顶点为![]() ;观光带的后一部分为线段BC,如图所示.
;观光带的后一部分为线段BC,如图所示.
(1)求曲线段OABC对应的函数![]() 的解析式;
的解析式;
(2)若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ,绿化带由线段MQ,QP, PN构成,其中点P在线段BC上.当OM长为多少时,绿化带的总长度最长?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数f(x)=4x2-2(t-2)x-2t2-t+1在区间[-1,1]内至少存在一个值m,使得f(m)>0,则实数t的取值范围( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了![]() 人进行分析,得到如下列联表(单位:人).
人进行分析,得到如下列联表(单位:人).
经常使用 | 偶尔使用或不使用 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)根据以上数据,能否在犯错误的概率不超过![]() 的前提下认为
的前提下认为![]() 市使用共享单车的情况与年龄有关;
市使用共享单车的情况与年龄有关;
(2)(i)现从所选取的![]() 岁以上的网友中,采用分层抽样的方法选取
岁以上的网友中,采用分层抽样的方法选取![]() 人,再从这
人,再从这![]() 人中随机选出
人中随机选出![]() 人赠送优惠券,求选出的
人赠送优惠券,求选出的![]() 人中至少有
人中至少有![]() 人经常使用共享单车的概率;
人经常使用共享单车的概率;
(ii)将频率视为概率,从![]() 市所有参与调查的网友中随机选取
市所有参与调查的网友中随机选取![]() 人赠送礼品,记其中经常使用共享单车的人数为
人赠送礼品,记其中经常使用共享单车的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式: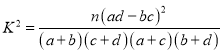 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,椭圆
,椭圆![]() :
:![]() 与双曲线
与双曲线![]() :
:![]() 的焦点相同.
的焦点相同.
(1)求椭圆![]() 与双曲线
与双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 的右顶点作两条斜率分别为
的右顶点作两条斜率分别为![]() ,
,![]() 的直线
的直线![]() ,
,![]() ,分别交双曲线
,分别交双曲线![]() 于点
于点![]() ,
,![]() (
(![]() ,
,![]() 不同于右顶点),若
不同于右顶点),若![]() ,求证:直线
,求证:直线![]() 的倾斜角为定值,并求出此定值;
的倾斜角为定值,并求出此定值;
(3)设点![]() ,若对于直线
,若对于直线![]() ,椭圆
,椭圆![]() 上总存在不同的两点
上总存在不同的两点![]() 与
与![]() 关于直线
关于直线![]() 对称,且
对称,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com