
【题目】设![]() ,椭圆
,椭圆![]() :
:![]() 与双曲线
与双曲线![]() :
:![]() 的焦点相同.
的焦点相同.
(1)求椭圆![]() 与双曲线
与双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 的右顶点作两条斜率分别为
的右顶点作两条斜率分别为![]() ,
,![]() 的直线
的直线![]() ,
,![]() ,分别交双曲线
,分别交双曲线![]() 于点
于点![]() ,
,![]() (
(![]() ,
,![]() 不同于右顶点),若
不同于右顶点),若![]() ,求证:直线
,求证:直线![]() 的倾斜角为定值,并求出此定值;
的倾斜角为定值,并求出此定值;
(3)设点![]() ,若对于直线
,若对于直线![]() ,椭圆
,椭圆![]() 上总存在不同的两点
上总存在不同的两点![]() 与
与![]() 关于直线
关于直线![]() 对称,且
对称,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)椭圆![]() 的方程为
的方程为![]() ,双曲线
,双曲线![]() 的方程为
的方程为![]() ;(2)详见解析.(3)见解析。
;(2)详见解析.(3)见解析。
【解析】
(1)利用椭圆和双曲线的性质,结合焦点相同,建立方程,计算m值,即可。(2)设出直线![]() 方程,代入双曲线方程,建立等式,计算P的坐标,同理得到Q的坐标,结合
方程,代入双曲线方程,建立等式,计算P的坐标,同理得到Q的坐标,结合![]() ,可以得到
,可以得到![]() ,发现直线PQ与x轴平行,故证之。(3)结合题意,设出直线AB的方程,代入椭圆解析式中,建立方程,计算出AB的中点M坐标,而M又在直线l上,代入,结合题目所提供的不等式,建立不等关系,即可得到b的范围。
,发现直线PQ与x轴平行,故证之。(3)结合题意,设出直线AB的方程,代入椭圆解析式中,建立方程,计算出AB的中点M坐标,而M又在直线l上,代入,结合题目所提供的不等式,建立不等关系,即可得到b的范围。
解:(1)由题意,![]() ,所以
,所以![]() .
.
所以椭圆![]() 的方程为
的方程为![]() ,双曲线
,双曲线![]() 的方程为
的方程为![]() .
.
(2)双曲线![]() 的右顶点为
的右顶点为![]() ,因为
,因为![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,
由![]() ,得
,得![]() ,
,
则![]() ,(
,(![]() ),
), .
.
同理,![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() ,
,![]() .
.
因为![]() ,所以直线
,所以直线![]() 与
与![]() 轴平行,即
轴平行,即![]() 为定值
为定值![]() ,倾斜角为0. ,
,倾斜角为0. ,
(3)设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
由 整理得
整理得![]() ,
,
△![]() ,故
,故![]() .
.
![]() ,
,![]() ,
,
设![]() 的中点为
的中点为![]() ,则
,则![]() ,
,![]() ,
,
又![]() 在直线
在直线![]()
![]() 上,所以
上,所以![]() ,
,![]() .
.
因为![]() ,
,![]() ,
,
所以![]()
![]()
![]() ,所以
,所以![]() .又
.又![]() ,
,![]() 。
。
即![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在区间
在区间![]() 上不单调,求实数
上不单调,求实数![]() 的取值范围;
的取值范围;
(3)求证:![]() 或
或![]() 是函数
是函数![]() 在
在![]() 上有三个不同零点的必要不充分条件.
上有三个不同零点的必要不充分条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月,河北、辽宁、江苏、福建、湖北、湖南、广东、重庆等8省市发布高考综合改革实施方案,决定从2018年秋季入学的高中一年级学生开始实施“![]() ”高考模式.所谓“
”高考模式.所谓“![]() ”,即“3”是指考生必选语文、数学、外语这三科;“1”是指考生在物理、历史两科中任选一科;“2”是指考生在生物、化学、思想政治、地理四科中任选两科.
”,即“3”是指考生必选语文、数学、外语这三科;“1”是指考生在物理、历史两科中任选一科;“2”是指考生在生物、化学、思想政治、地理四科中任选两科.
(1)若某考生按照“![]() ”模式随机选科,求选出的六科中含有“语文,数学,外语,物理,化学”的概率.
”模式随机选科,求选出的六科中含有“语文,数学,外语,物理,化学”的概率.
(2)新冠疫情期间,为积极应对“![]() ”新高考改革,某地高一年级积极开展线上教学活动.教育部门为了解线上教学效果,从当地不同层次的学校中抽取高一学生2500名参加语数外的网络测试,并给前400名颁发荣誉证书,假设该次网络测试成绩服从正态分布,且满分为450分.
”新高考改革,某地高一年级积极开展线上教学活动.教育部门为了解线上教学效果,从当地不同层次的学校中抽取高一学生2500名参加语数外的网络测试,并给前400名颁发荣誉证书,假设该次网络测试成绩服从正态分布,且满分为450分.
①考生甲得知他的成绩为270分,考试后不久了解到如下情况:“此次测试平均成绩为171分,351分以上共有57人”,请用你所学的统计知识估计甲能否获得荣誉证书,并说明理由;
②考生丙得知他的实际成绩为430分,而考生乙告诉考生丙:“这次测试平均成绩为201分,351分以上共有57人”,请结合统计学知识帮助丙同学辨别乙同学信息的真伪,并说明理由.
附:![]() ;
;
![]() ;
;
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,其中点
两点,其中点![]() 的坐标为
的坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,作直线
,作直线![]() .
.
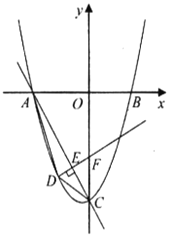
(1)求抛物线的解析式;
(2)如图,点![]() 是直线
是直线![]() 下方抛物线上的一个动点,连结
下方抛物线上的一个动点,连结![]() .当
.当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)如图,在(2)的条件下,过点![]() 作于
作于![]() 点
点![]() 交
交![]() 轴于点
轴于点![]() 将
将![]() 绕点
绕点![]() 旋转得到
旋转得到![]() 在旋转过程中,当点
在旋转过程中,当点![]() 或点
或点![]() 落在
落在![]() 轴上(不与点
轴上(不与点![]()
![]() 重合)时,将
重合)时,将![]() 沿射线
沿射线![]() 平移得到
平移得到![]() ,在平移过程中,平面内是否存在点
,在平移过程中,平面内是否存在点![]() 使得四边形
使得四边形![]() 是菱形?若存在,请直接写出所有符合条件的点
是菱形?若存在,请直接写出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 为等腰三角形,
为等腰三角形,![]() ,平面
,平面![]() 平面
平面![]() ,动点
,动点![]() 在棱
在棱![]() 上,无论点
上,无论点![]() 运动到何处时,总有
运动到何处时,总有![]() .
.
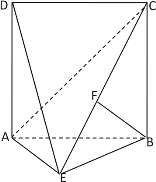
(1)试判断平面![]() 与平面
与平面![]() 是否垂直,并证明你的结论;
是否垂直,并证明你的结论;
(2)若点![]() 为
为![]() 中点,求三棱锥
中点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天津市某高中团委在2019年12月4日开展了以“学法、遵法、守法”为主题的学习活动.为检查该学校组织学生学习的效果,现从该校高一、高二、高三的学生中分别选取了4人,3人,3人作为代表进行问卷测试.具体要求:每位学生要从10个有关法律、法规的问题中随机抽出4个问题进行作答.
(1)若从这10名学生中任选3人,求这3名学生分别来自三个年级的概率;
(2)若这10人中的某学生能答对10道题中的7道题,另外3道题回答不对,记![]() 表示该名学生答对问题的个数,求随机变量
表示该名学生答对问题的个数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】焦距为![]() 的椭圆
的椭圆![]() (
(![]() ),如果满足“
),如果满足“![]() ”,则称此椭圆为“等差椭圆”.
”,则称此椭圆为“等差椭圆”.
(1)如果椭圆![]() (
(![]() )是“等差椭圆”,求
)是“等差椭圆”,求![]() 的值;
的值;
(2)如果椭圆![]() (
(![]() )是“等差椭圆”,过
)是“等差椭圆”,过![]() 作直线
作直线![]() 与此“等差椭圆”只有一个公共点,求此直线的斜率;
与此“等差椭圆”只有一个公共点,求此直线的斜率;
(3)椭圆![]() (
(![]() )是“等差椭圆”,如果焦距为12,求此“等差椭圆”的方程;
)是“等差椭圆”,如果焦距为12,求此“等差椭圆”的方程;
(4)对于焦距为12的“等差椭圆”,点![]() 为椭圆短轴的上顶点,
为椭圆短轴的上顶点,![]() 为椭圆上异于
为椭圆上异于![]() 点的任一点,
点的任一点,![]() 为
为![]() 关于原点
关于原点![]() 的对称点(
的对称点(![]() 也异于
也异于![]() ),直线
),直线![]()
![]() 分别与
分别与![]() 轴交于
轴交于![]()
![]() 两点,判断以线段
两点,判断以线段![]() 为直径的圆是否过定点?说明理由.
为直径的圆是否过定点?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com