
【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:

(1)填写下表:
平均数 | 方差 | 中位数 | 命中9环及以上 | |
甲 | 7 | 1.2 | 1 | |
乙 | 5.4 | 3 |
(2)请从四个不同的角度对这次测试进行①结合平均数和方差分析离散程度;②结合平均数和中位数分析谁的成绩好些;③结合平均数和命中9环及以上的次数看谁的成绩好些;④从折线图上看两人射靶命中环数及走势分析谁更有潜力.
【答案】(1)列联表见解析;(2)见解析.
【解析】
(1)从图上读出甲乙两人的10个数据,计算均值、方差,中位数等后可填表;
(2)由于均值相等,因此方差大小反映离散程度,中位数反映成绩好坏,命环数多的次数也反映成绩好坏,折线的趋势能反映个人的潜力大小.
(1)乙的射靶环数依次为2,4,6,8,7,7,8,9,9,10.所以![]() ;乙的射靶环数从小到大排列为2,4,6,7,7,8,8,9,9,10,所以中位数是
;乙的射靶环数从小到大排列为2,4,6,7,7,8,8,9,9,10,所以中位数是![]() ;甲的射靶环数从小到大排列为5,6,6,7,7,7,7,8,8,9,所以中位数为7.于是填充后的表格如下表所示:
;甲的射靶环数从小到大排列为5,6,6,7,7,7,7,8,8,9,所以中位数为7.于是填充后的表格如下表所示:
平均数 | 方差 | 中位数 | 命中9环及以上 | |
甲 | 7 | 1.2 | 7 | 1 |
乙 | 7 | 5.4 | 7.5 | 3 |
(2)①甲、乙的平均数相同,均为7,但![]() ,说明甲离散程度小,而乙离散程度大.
,说明甲离散程度小,而乙离散程度大.
②甲、乙的平均水平相同,而乙的中位数比甲大,说明乙射靶成绩比甲好.
③甲、乙的平均水平相同,而乙命中9环及以上的次数比甲多2次,可知乙的射靶成绩比甲好.
④从折线图上看,乙的成绩呈上升趋势,而甲的成绩在平均线上波动不大,说明乙的状态在提升,更有潜力.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .将
.将![]() 的图象向左平移
的图象向左平移![]() 个单位长度后所得的函数为偶函数,则关于函数
个单位长度后所得的函数为偶函数,则关于函数![]() ,下列命题正确的是( )
,下列命题正确的是( )
A. 函数![]() 在区间
在区间![]() 上有最小值 B. 函数
上有最小值 B. 函数![]() 在区间
在区间![]() 上单调递增
上单调递增
C. 函数![]() 的一条对称轴为
的一条对称轴为![]() D. 函数
D. 函数![]() 的一个对称点为
的一个对称点为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数:f(x)=x2﹣mx﹣n(m, n∈R).
(1)若m+n=0,解关于x的不等式f(x)≥x(结果用含m式子表示);
(2)若存在实数m,使得当x∈[1,2]时,不等式x≤f(x)≤4x恒成立,求实数n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强市民节能环保意识,某市面向全市征召义务宣传志愿者,现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示:
分组(单位:岁) | 频数 | 频率 |
| 5 | 0.05 |
| ① | 0.20 |
| 35 | ② |
| 30 | 0.30 |
| 10 | 0.10 |
总计 | 100 | 1.00 |

(1)频率分布表中的①②位置应填什么数据?
(2)补全如图所示的频率分布直方图,再根据频率分布直方图估计这500名志愿者中年龄在![]() 岁的人数.
岁的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 及点
及点![]() ,若直线
,若直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,且
,且![]() (
( ![]() 为坐标原点),椭圆
为坐标原点),椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全国第五个“扶贫日”到来之前,某省开展“精准扶贫,携手同行”的主题活动,某贫困县调查基层干部走访贫困户数量.![]() 镇有基层干部60人,
镇有基层干部60人,![]() 镇有基层干部60人,
镇有基层干部60人,![]() 镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从
镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从![]() 三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,
三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
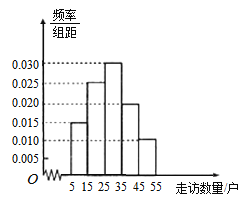
(1)求这40人中有多少人来自![]() 镇,并估计
镇,并估计![]() 三镇的基层干部平均每人走访多少贫困户;(同一组中的数据用该组区间的中点值作代表)
三镇的基层干部平均每人走访多少贫困户;(同一组中的数据用该组区间的中点值作代表)
(2)如果把走访贫困户达到或超过25户视为工作出色,以频率估计概率,从![]() 三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为
三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较注射![]() 两种药物产生的皮肤疱疹的面积,选200只家兔作试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物
两种药物产生的皮肤疱疹的面积,选200只家兔作试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物![]() ,另一组注射药物
,另一组注射药物![]() .表1和表2所示的分别是注射药物
.表1和表2所示的分别是注射药物![]() 和药物
和药物![]() 后皮肤疱疹面积的频数分布(疱疹面积单位:
后皮肤疱疹面积的频数分布(疱疹面积单位:![]() )
)
表1
疱疹面积 |
|
|
|
|
频数 | 30 | 40 | 20 | 10 |
表2
疱疹面积 |
|
|
|
|
|
频数 | 10 | 25 | 20 | 30 | 15 |
(1)完成图20-3和图20-4所示的分别注射药物![]() 后皮肤疱疹面积的频率分布直方图,并求注射药物
后皮肤疱疹面积的频率分布直方图,并求注射药物![]() 后疱疹面积的中位数
后疱疹面积的中位数

(2)完成下表所示的![]() 列联表,并回答能否有99.9%的把握认为注射药物
列联表,并回答能否有99.9%的把握认为注射药物![]() 后的疱疹面积与注射药物
后的疱疹面积与注射药物![]() 的疱疹面积有差异.(
的疱疹面积有差异.(![]() 的值精确到0.01)
的值精确到0.01)
疱疹面积小于 | 疱疹面积不小于 | 合计 | |
注射药物A |
|
| |
注射药物B |
|
| |
合计 |
附: .
.
P( | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.811 | 5.021 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com