
【题目】在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,且
边上,且![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,求
,求![]() 的周长.
的周长.
【答案】(1) ![]() .
.
(2) ![]() .
.
【解析】分析:首先应用题中条件,结合余弦定理求得![]() ,第一问利用余弦定理和正弦定理,以及结合边的关系,求得
,第一问利用余弦定理和正弦定理,以及结合边的关系,求得![]() 以及
以及![]() ,结合同角三角函数关系式,求得
,结合同角三角函数关系式,求得![]() 的值,第二问结合边的关系,结合余弦定理求得其周长的值.
的值,第二问结合边的关系,结合余弦定理求得其周长的值.
详解:解法一:如图,已知![]() ,
,![]() ,
,
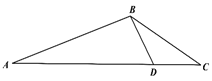
所以![]() ,则
,则![]() .
.
在△![]() 中,根据余弦定理,
中,根据余弦定理,![]() ,
,
所以![]() .
.
(1)在△![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由余弦定理![]() ,
,
所以![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
在△![]() 中,由正弦定理
中,由正弦定理![]() ,
,
所以![]() ,
,![]() ,
,
由![]() ,
,![]() ,
,![]() ,在△
,在△![]() 中,由
中,由![]() ,得
,得
![]() ,故
,故![]() ,
,
所以![]() ,
,
所以![]()
(2)设![]() ,则
,则![]() ,从而
,从而![]() ,
,
故![]() .
.
在△![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
因为![]() ,所以
,所以![]() ,解得
,解得![]() .
.
所以![]() .故△
.故△![]() 周长为
周长为![]() .
.
解法二:如图,已知![]() ,
,![]() ,所以
,所以![]() ,则
,则![]() .
.
在△![]() 中,根据余弦定理,
中,根据余弦定理,![]() ,
,
所以![]() .
.
(1)在△![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由余弦定理![]() ,
,
所以![]() ,解得
,解得![]() ,
,
由余弦定理![]() ,
,
又因为![]() ,所以
,所以![]() .
.
所以![]() ,
,
所以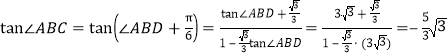 .
.
(2)同解法一.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:

(1)填写下表:
平均数 | 方差 | 中位数 | 命中9环及以上 | |
甲 | 7 | 1.2 | 1 | |
乙 | 5.4 | 3 |
(2)请从四个不同的角度对这次测试进行①结合平均数和方差分析离散程度;②结合平均数和中位数分析谁的成绩好些;③结合平均数和命中9环及以上的次数看谁的成绩好些;④从折线图上看两人射靶命中环数及走势分析谁更有潜力.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 命题![]() :存在
:存在![]() ,使
,使![]() ,则非
,则非![]() :对任意
:对任意![]() ,都有
,都有![]() ;
;
B. 如果命题“![]() 或
或![]() ”与命题“非
”与命题“非![]() ”都是真命题,那么命题
”都是真命题,那么命题![]() 一定是真命题;
一定是真命题;
C. 命题“若![]() 都是偶数,则
都是偶数,则![]() 是偶数”的逆否命题是“若
是偶数”的逆否命题是“若![]() 不是偶数,则
不是偶数,则![]() 不是偶数”;
不是偶数”;
D. 命题“存在![]() ,
,![]() ”是假命题
”是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把标号为1,2,3,4的四张卡片分发给甲、乙、丙、丁四个人,每人1张,事件A表示随机事件“甲分得1号卡片”,事件B表示随机事件“乙分得1号卡片”.
(1)![]() 分别指什么事件?
分别指什么事件?
(2)事件A与事件B是否为互斥事件?若是互斥事件,则是否互为对立事件?若不是对立事件,请分别说出事件A、事件B的对立事件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把6本不同的书,全部分给甲,乙,丙三人,在下列不同情形下,各有多少种分法?(用数字作答)
(Ⅰ)甲得2本;
(Ⅱ)每人2本;
(Ⅲ)有1人4本,其余两人各1本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6, 0.5,0.5,0.4,各人是否使用设备相互独立,
(1)求同一工作日至少3人需使用设备的概率;
(2)实验室计划购买k台设备供甲、乙、丙、丁使用,若要求“同一工作日需使用设备的人数大于k”的概率小于0.1,求k的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com