
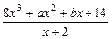 ,定义域为[-1,1]
,定义域为[-1,1]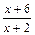 均成立,求实数a,b的值.
均成立,求实数a,b的值. 时,f(x)取到最小值6.
时,f(x)取到最小值6. 
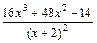
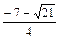 ,x=
,x=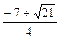 ,或x=
,或x= .
.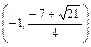 或
或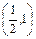 ,则f′(x)>0,即f(x)在
,则f′(x)>0,即f(x)在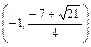 和
和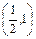 上为增函数.
上为增函数.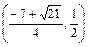 ,则f′(x)<0,即f(x)在
,则f′(x)<0,即f(x)在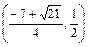 上为减函数,
上为减函数, )=6为极小值.
)=6为极小值. )=6.
)=6. 时,f(x)取到最小值6.
时,f(x)取到最小值6.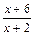
 6≤
6≤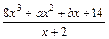 ≤5+
≤5+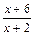
 6(x+2)≤8x3+ax2+6x+14≤6x+16
6(x+2)≤8x3+ax2+6x+14≤6x+16 0≤8x3+ax2+(b-6)x+2≤4
0≤8x3+ax2+(b-6)x+2≤4
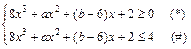
 ,得
,得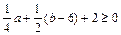
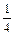 a+
a+ b≥0
b≥0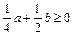 (2)
(2) ,得
,得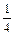 a-
a- (b-6)+2≤4
(b-6)+2≤4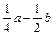 ≤0
≤0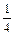 a+
a+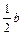 ≥0 (4)
≥0 (4)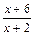
 0≤8x3+ax2+(b-6)x+2≤4
0≤8x3+ax2+(b-6)x+2≤4 0≤8x3-6x+2≤4
0≤8x3-6x+2≤4 0≤g(x)≤4
0≤g(x)≤4 或x=
或x= .
.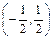 或
或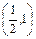 则g′(x)>0,即g(x)在
则g′(x)>0,即g(x)在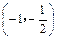 和
和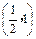 上为增函数.
上为增函数.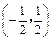 ,则g′(x)<0,即g(x)在
,则g′(x)<0,即g(x)在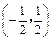 上为减函数,
上为减函数,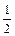 )=4为极大值,g(
)=4为极大值,g(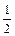 )=0为极小值.
)=0为极小值.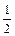 )=g(1)=4,
)=g(1)=4,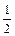 )=0.
)=0.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源:不详 题型:解答题
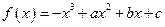 在
在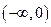 上是减函数,在
上是减函数,在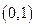 上是增函数,函数
上是增函数,函数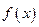 在
在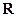 上有三个零点,且1是其中一个零点.
上有三个零点,且1是其中一个零点.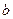 的值;
的值;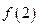 的取值范围;
的取值范围;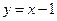 与函数
与函数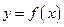 的图像交点个数的情况,并说明理由.
的图像交点个数的情况,并说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
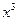 -ax在[1,+∞)上是单调函数.
-ax在[1,+∞)上是单调函数. ≥1,f(x)≥1,且f(f(
≥1,f(x)≥1,且f(f( ))=
))= ,求证:f(
,求证:f( )=
)= .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
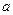
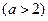 ,E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积。
,E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积。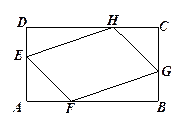
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的图象上任意两点,且
的图象上任意两点,且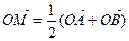 ,已知点M的横坐标为
,已知点M的横坐标为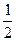 .
.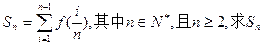 ;
;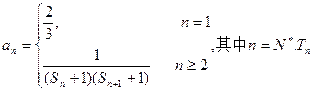 为数列
为数列 的前n项和,若
的前n项和,若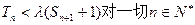 都成立,试求
都成立,试求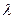 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
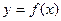 ,若同时满足下列条件:
,若同时满足下列条件: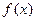 在D内单调递增或单调递减;
在D内单调递增或单调递减; ]
]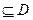 ,使
,使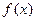 在[
在[ ]上的值域为[
]上的值域为[ ];那么把
];那么把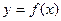 (
(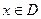 )叫闭函数。
)叫闭函数。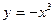 符合条件②的区间[
符合条件②的区间[ ];
];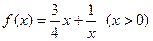 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;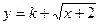 是闭函数,求实数
是闭函数,求实数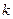 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
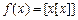 ,其中
,其中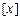 表示不超过x的最大整数,如:
表示不超过x的最大整数,如: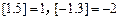 ,当
,当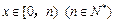 时,设函数
时,设函数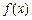 的值域为A,记集合A中的元素个数为an,则式子
的值域为A,记集合A中的元素个数为an,则式子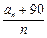 的最小值为( )
的最小值为( )| A.10 | B.13 | C.14 | D.16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com