
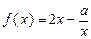
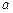
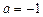 时,求函数
时,求函数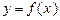 的值域;
的值域;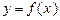 在定义域上是减函数,求
在定义域上是减函数,求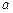 的取值范围;
的取值范围;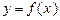 在x∈(0,1]上的最大值及最小值,并求出函数取最值时
在x∈(0,1]上的最大值及最小值,并求出函数取最值时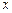 的值
的值科目:高中数学 来源:不详 题型:解答题
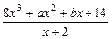 ,定义域为[-1,1]
,定义域为[-1,1]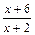 均成立,求实数a,b的值.
均成立,求实数a,b的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 地10台,
地10台, 地8台.已知从甲地调动1台至
地8台.已知从甲地调动1台至 地,
地, 地的运费分别为400元和800元,从乙地调运1台至
地的运费分别为400元和800元,从乙地调运1台至 地,
地, 地的费用分别为300元和500元.
地的费用分别为300元和500元.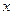 台至
台至 地,求总费用
地,求总费用 关于台数
关于台数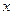 的函数解析式;
的函数解析式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
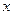 m处的大气压强是
m处的大气压强是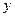 Pa,
Pa,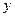 与
与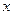 之间的函数关系式是
之间的函数关系式是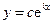 ,其中
,其中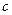 ,
,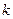 为常量.测得某地某天海平面的大气压强为
为常量.测得某地某天海平面的大气压强为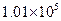 Pa,1000m高空的大气压为
Pa,1000m高空的大气压为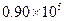 Pa,求600m高空的大气压强(保留
Pa,求600m高空的大气压强(保留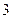 个有效数字).
个有效数字).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 是该行星绕太阳一周所需的时间.每一行星轨道的半长轴是该行星与太阳之间的最大距离和最小距离的平均值.开普勒发现行星的周期与它的半长轴的
是该行星绕太阳一周所需的时间.每一行星轨道的半长轴是该行星与太阳之间的最大距离和最小距离的平均值.开普勒发现行星的周期与它的半长轴的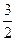 次幂成正比.距离太阳最近的水星,其半长轴为5800万千米,水星的运行周期约为88天.距离太阳最远的冥王星,其半长轴为60亿千米,冥王星的运行周期是多少(以年计)?地球轨道的半长轴为
次幂成正比.距离太阳最近的水星,其半长轴为5800万千米,水星的运行周期约为88天.距离太阳最远的冥王星,其半长轴为60亿千米,冥王星的运行周期是多少(以年计)?地球轨道的半长轴为 亿千米,地球的运行周期是多少(以年计)?
亿千米,地球的运行周期是多少(以年计)?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com