
 地10台,
地10台, 地8台.已知从甲地调动1台至
地8台.已知从甲地调动1台至 地,
地, 地的运费分别为400元和800元,从乙地调运1台至
地的运费分别为400元和800元,从乙地调运1台至 地,
地, 地的费用分别为300元和500元.
地的费用分别为300元和500元.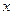 台至
台至 地,求总费用
地,求总费用 关于台数
关于台数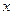 的函数解析式;
的函数解析式;科目:高中数学 来源:不详 题型:解答题
 的图象上任意两点,且
的图象上任意两点,且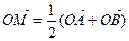 ,已知点M的横坐标为
,已知点M的横坐标为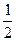 .
.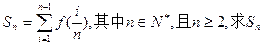 ;
;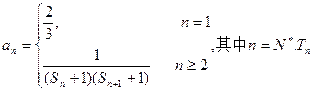 为数列
为数列 的前n项和,若
的前n项和,若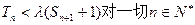 都成立,试求
都成立,试求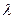 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
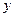 (单位:万元)随销售利润
(单位:万元)随销售利润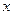 (单位:万元)的增加而增加,但奖金总数不超过
(单位:万元)的增加而增加,但奖金总数不超过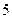 万元,同时奖金不超过利润的
万元,同时奖金不超过利润的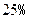 .现有三个奖励模型:
.现有三个奖励模型: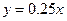 ,
,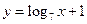 ,
,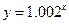 .其中哪个模型能符合公司的要求?
.其中哪个模型能符合公司的要求?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com