
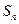 为数列
为数列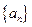 的前
的前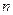 项和,且
项和,且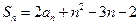 ,
,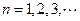 ,(Ⅰ)求证:数列
,(Ⅰ)求证:数列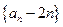 为等比数列;(Ⅱ)设
为等比数列;(Ⅱ)设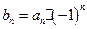 ,求数列
,求数列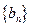 的前
的前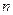 项和
项和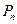 ;(Ⅲ)设
;(Ⅲ)设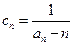 ,数列
,数列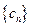 的前
的前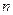 项和为
项和为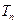 ,求证:
,求证: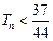 .
. 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源:不详 题型:解答题
 是
是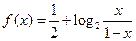 的图象上任意两点,设点
的图象上任意两点,设点 ,且
,且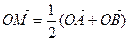 ,若
,若 ,其中
,其中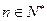 ,且
,且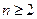 。
。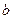 的值;
的值;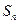 ;
;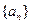 中
中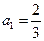 ,当
,当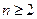 时,
时,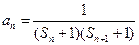 ,设数列
,设数列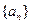 的前
的前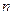 项和为
项和为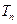 ,
,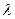 的取值范围使
的取值范围使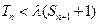 对一切
对一切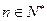 都成立。
都成立。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
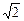 cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.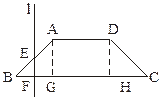
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 地10台,
地10台, 地8台.已知从甲地调动1台至
地8台.已知从甲地调动1台至 地,
地, 地的运费分别为400元和800元,从乙地调运1台至
地的运费分别为400元和800元,从乙地调运1台至 地,
地, 地的费用分别为300元和500元.
地的费用分别为300元和500元.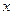 台至
台至 地,求总费用
地,求总费用 关于台数
关于台数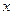 的函数解析式;
的函数解析式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
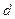 cm,高是
cm,高是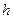 cm.现在以
cm.现在以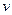 cm
cm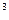 /s的速度向容器内注入某种溶液.求容器内溶液的高度
/s的速度向容器内注入某种溶液.求容器内溶液的高度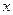 cm与注入溶液的时间
cm与注入溶液的时间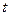 s之间的函数解析式,并写出函数的定义域和值域.
s之间的函数解析式,并写出函数的定义域和值域.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com