
| 11 |
| 2 |
| 20×19 |
| 2 |
| 5×4 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
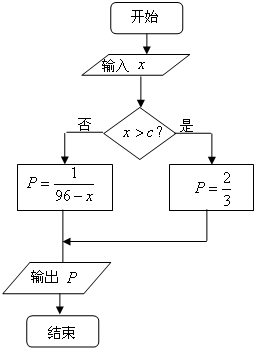 某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率p与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率P=
某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率p与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率P=| 次品数 |
| 生产量 |
| A |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com