练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】执行如图的程序框图，则输出K的值为（ ）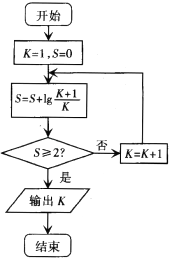
    A.98
    B.99
    C.100
    D.101

    【答案】B
    【解析】解：模拟程序的运行，可得 K=1，S=0
    S=lg2
    不满足条件S≥2，执行循环体，K=2，S=lg2+lg =lg3
    不满足条件S≥2，执行循环体，K=3，S=lg3+lg =lg4
    …
    观察规律，可得：
    不满足条件S≥2，执行循环体，K=99，S=lg99+lg =lg100=2
    满足条件S≥2，退出循环，输出K的值为99．
    故选：B．
    【考点精析】解答此题的关键在于理解程序框图的相关知识，掌握程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必要文字说明．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥P﹣ABC中，AB=AC=PB=PC=10，PA=8，BC=12，点M在平面PBC内，且AM=7，设异面直线AM与BC所成角为α，则cosα的最大值为（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x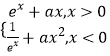）= ，若函数f（x）有四个零点，则实数a的取值范围是（ ）
    A.（﹣∞，﹣e）
    B.（﹣∞，﹣ ）
    C.（﹣∞，﹣ ）
    D.（﹣∞，﹣ ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C的离心率为 ，F1 ， F2分别为椭圆的左右焦点，P为椭圆上任意一点，△PF1F2的周长为 ，直线l：y=kx+m（k≠0）与椭圆C相交于A，B两点． （Ⅰ）求椭圆C的标准方程；
    （Ⅱ）若直线l与圆x2+y2=1相切，过椭圆C的右焦点F2作垂直于x轴的直线，与椭圆相交于M，N两点，与线段AB相交于一点（与A，B不重合）．求四边形MANB面积的最大值及取得最大值时直线l的方程；
    （Ⅲ）若|AB|=2，试判断直线l与圆x2+y2=1的位置关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一次购物抽奖活动中，假设某10张券中有一等奖券1张，可获价值50元的奖品；有二等奖券3张，每张可获价值10元的奖品；其余6张没有奖，某顾客从此10张券中任抽2张，求：
    （Ⅰ）该顾客中奖的概率；
    （Ⅱ）该顾客获得的奖品总价值ξ（元）的概率分布列和期望Eξ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设样本数据x1 ， x2 ， …，x2017的方差是4，若yi=2xi﹣1（i=1，2，…，2017），则y1 ， y2 ， …y2017的方差为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=mln（x+1），g（x）= （x＞﹣1）．
    （Ⅰ）讨论函数F（x）=f（x）﹣g（x）在（﹣1，+∞）上的单调性；
    （Ⅱ）若y=f（x）与y=g（x）的图象有且仅有一条公切线，试求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-4：坐标系与参数方程]

    在直角坐标系xoy中，曲线C1的参数方程为 （β为参数）．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=4cosθ．
    （Ⅰ）将曲线C1的方程化为极坐标方程；
    （Ⅱ）已知直线l的参数方程为 （ ＜α＜π，t为参数，t≠0），l与C1交与点A，l与C2交与点B，且|AB|= ，求α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在实数集R上的函数f（x）满足f（x+1）= + ，则f（0）+f（2017）的最大值为（ ）
    A.1﹣
    B.1+
    C.
    D.

    查看答案和解析>>

    同步练习册答案