Question

【题目】如图，在三棱锥P﹣ABC中，AB=AC=PB=PC=10，PA=8，BC=12，点M在平面PBC内，且AM=7，设异面直线AM与BC所成角为α，则cosα的最大值为（ ）

A.
B.
C.
D.

Answer 1

【答案】A
【解析】解：取BC中点N，连结AN，PN，∵AB=AC=PB=PC=10，BC=12，∴AN=PN=8，
∵PA=8，∴△PAN是等边三角形，∠ANP=60°．
∵AN⊥BC，PN⊥BC，∴∠ANP为二面角A﹣BC﹣P的平面角．
过A作AO⊥平面PBC，连结OM，则O为PN的中点，∴ON= PN=4，∴AO= =4 ．
∴OM= =1．∴M的轨迹是以O为圆心，以1为半径的圆．
以平面PBC内过O点平行于BC的直线为x轴，以PN为y轴，以OA为z轴建立空间直角坐标系如图．
则A（0，0，4 ），B（﹣6，4，0），C（6，4，0），设M（x，y，0），则x2+y2=1．
=（x，y，﹣4 ）， =（12，0，0）．| |=7，| |=12， =12x．
∴cosα= = = ．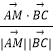
∴当x=1时，cosα取得最大值 ．
故选A．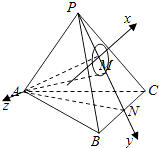

【考点精析】掌握异面直线及其所成的角是解答本题的根本，需要知道异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系．