
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是 (t是参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线
(t是参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() 。
。
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若两曲线交点为![]() ,求
,求![]()
科目:高中数学 来源: 题型:
【题目】已知动圆过定点P(4,0),且在y轴上截得的弦MN的长为8.
(1)求动圆圆心C的轨迹方程;
(2)过点(2,0)的直线l与动圆圆心C的轨迹交于A,B两点,求证:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]()
![]() ,焦点
,焦点![]() ,如果存在过点
,如果存在过点![]()
![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() .
.![]() ,使得
,使得![]() ,则称点
,则称点![]() 为抛物线
为抛物线![]() 的“
的“![]() 分点”.
分点”.
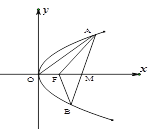
(1)如果![]() ,直线
,直线![]() :
:![]() ,求
,求![]() 的值;
的值;
(2)如果![]() 为抛物线
为抛物线![]() 的“
的“![]() 分点”,求直线
分点”,求直线![]() 的方程;
的方程;
(3)证明点![]() 不是抛物线
不是抛物线![]() 的“2分点”;
的“2分点”;
(4)如果![]()
![]() 是抛物线的“2分点”,求
是抛物线的“2分点”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹,用于装点生活或配合其他民俗活动的民间艺术;蕴含了极致的数学美和丰富的传统文化信息,现有一幅剪纸的设计图,其中的4个小圆均过正方形的中心,且内切于正方形的两邻边.若在正方形内随机取一点,则该点取自黑色部分的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着电子商务的兴起,网上销售为人们带来了诸多便利.商务部预计,到2020年,网络销售占比将达到![]() .网购的发展同时促进了快递业的发展,现有甲、乙两个快递公司,每位打包工平均每天打包数量在
.网购的发展同时促进了快递业的发展,现有甲、乙两个快递公司,每位打包工平均每天打包数量在![]() 范围内.为扩展业务,现招聘打包工.两公司提供的工资方案如下:甲公司打包工每天基础工资64元,且每天每打包一件快递另赚1元;乙公司打包工无基础工资,如果每天打包量不超过240件,则每打包一件快递可赚1.2元;如果当天打包量超过240件,则超出的部分每件赚1.8元.
范围内.为扩展业务,现招聘打包工.两公司提供的工资方案如下:甲公司打包工每天基础工资64元,且每天每打包一件快递另赚1元;乙公司打包工无基础工资,如果每天打包量不超过240件,则每打包一件快递可赚1.2元;如果当天打包量超过240件,则超出的部分每件赚1.8元.
下图为随机抽取的打包工每天需要打包数量的频率分布直方图,以打包量的频率作为各打包量发生的概率.(同一组中的数据用该组区间的中间值作代表).
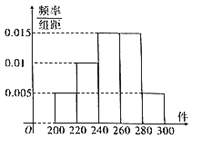
(1)(i)以每天打包量为自变量![]() ,写出乙公司打包工的收入函数
,写出乙公司打包工的收入函数![]() ;
;
(ii)若打包工小李是乙公司员工,求小李一天收入不低于324元的概率;
(2)某打包工在甲、乙两个快递公司中选择一个公司工作,如果仅从日平均收入的角度考虑,请利用所学的统计学知识为该打包工作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为
所表示的曲线为![]() ,则下面四个选项中错误的是( )
,则下面四个选项中错误的是( )
A.若![]() 为椭圆,则
为椭圆,则![]() B.若
B.若![]() 是双曲线,则其离心率有
是双曲线,则其离心率有![]()
C.若![]() 为双曲线,则
为双曲线,则![]() 或
或![]() D.若
D.若![]() 为椭圆,且长轴在
为椭圆,且长轴在![]() 轴上,则
轴上,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,过点C的直线与线段
中,过点C的直线与线段![]() 、
、![]() 分别相交于点M、N,若
分别相交于点M、N,若![]() ,
,![]() ;
;
(1)求y关于x的函数解析式;
(2)定义函数![]() (
(![]() ),点列
),点列![]() (
(![]() ,
,![]() )在函数
)在函数![]() 的图像上,且数列
的图像上,且数列![]() 是以1为首项,0.5为公比的等比数列,O为原点,令
是以1为首项,0.5为公比的等比数列,O为原点,令![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() ?若存在,求出Q点的坐标,若不存在,说明理由;
?若存在,求出Q点的坐标,若不存在,说明理由;
(3)设函数![]() 为
为![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() ,又函数
,又函数![]() 的图像关于直线
的图像关于直线![]() 对称,当方程
对称,当方程![]() 在
在![]() (
(![]() )上有两个不同的实数解时,求实数a的取值范围;
)上有两个不同的实数解时,求实数a的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com