
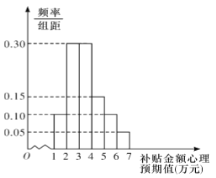
【题目】购买一辆某品牌新能源汽车,在行驶三年后,政府将给予适当金额的购车补贴.某调研机构对拟购买该品牌汽车的消费者,就购车补贴金额的心理预期值进行了抽样调查,其样本频率分布直方图如图所示
.
(1)估计拟购买该品牌汽车的消费群体对购车补贴金额的心理预期值的方差(同一组中的数据用该组区间的中点值作代表);
(2)将频率视为概率,从拟购买该品牌汽车的消费群体中随机抽取![]() 人,记对购车补贴金额的心理预期值高于
人,记对购车补贴金额的心理预期值高于![]() 万元的人数为
万元的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)统计最近![]() 个月该品牌汽车的市场销售量,得其频数分布表如下:
个月该品牌汽车的市场销售量,得其频数分布表如下:
月份 |
|
|
|
|
|
销售量(万辆) |
|
|
|
|
|
试预计该品牌汽车在![]() 年
年![]() 月份的销售量约为多少万辆?
月份的销售量约为多少万辆?
附:对于一组样本数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
【答案】(1)1.7;(2)![]() ,见解析;(2)2.
,见解析;(2)2.
【解析】
(1)平均数的估计值为每个小矩形组中值乘以小矩形面积的和;
(2)易得![]() ,由二项分布列的期望公式计算;
,由二项分布列的期望公式计算;
(3)利用所给公式计算出回归直线![]() 即可解决.
即可解决.
(1)由频率分布直方图可知,消费群体对购车补贴金额的心理预期值的平均数的估计值为
![]() ,所以方差的估计
,所以方差的估计
值为![]()
![]()
![]()
![]()
![]()
![]() ;
;
(2)由频率分布直方图可知,消费群体对购车补贴金额的心理预期值高于3万元的
频率为![]() ,则
,则![]() ,所以
,所以![]() 的分布列为
的分布列为
![]() ,数学期望
,数学期望![]() ;
;
(3)将 2018年11月至2019年3月的月份数依次编号为 1,2,3,4,5,
记 ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,由 散 点 图可知,
,由 散 点 图可知,
5组样本数据呈线性相关关系,因为![]() ,
,![]() ,
,![]()
![]() ,
,
![]() ,则
,则![]() ,
,![]() ,
,
所以回归直线方程为![]() ,当
,当![]() 时,
时,![]() ,预计该品
,预计该品
牌汽车在![]() 年
年![]() 月份的销售量约为2万辆.
月份的销售量约为2万辆.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|,a∈R.
(1)当f(2)+f(﹣2)>4时,求a的取值范围;
(2)若a>0,x,y∈(﹣∞,a],不等式f(x)≤|y+3|+|y﹣a|恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 表示
表示![]() ,
,![]() 中的最大值,如
中的最大值,如![]()
![]() .已知函数
.已知函数![]() ,
,![]() .
.
(1)设![]() ,求函数
,求函数![]() 在
在![]() 上零点的个数;
上零点的个数;
(2)试探讨是否存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)既是二次函数又是幂函数,函数g(x)是R上的奇函数,函数![]() =
=![]() +1,则h(2018)+h(2017)+h(2016)+…+h(1)+h(0)+h(﹣1)+…h(﹣2016)+h(﹣2017)+h(﹣2018)=___________
+1,则h(2018)+h(2017)+h(2016)+…+h(1)+h(0)+h(﹣1)+…h(﹣2016)+h(﹣2017)+h(﹣2018)=___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元五世纪,数学家祖冲之估计圆周率![]() 的值的范围是:3.1415926<
的值的范围是:3.1415926<![]() <3.1415927,为纪念祖冲之在圆周率的成就,把3.1415926称为“祖率”,这是中国数学的伟大成就.某小学教师为帮助同学们了解“祖率”,让同学们把小数点后的7位数字1,4,1,5,9,2,6进行随机排列,整数部分3不变,那么可以得到大于3.14的不同数字有( )
<3.1415927,为纪念祖冲之在圆周率的成就,把3.1415926称为“祖率”,这是中国数学的伟大成就.某小学教师为帮助同学们了解“祖率”,让同学们把小数点后的7位数字1,4,1,5,9,2,6进行随机排列,整数部分3不变,那么可以得到大于3.14的不同数字有( )
A.2280B.2120C.1440D.720
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)如图,长方形材料![]() 中,已知
中,已知![]() ,
,![]() .点
.点![]() 为材料
为材料![]() 内部一点,
内部一点,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() . 现要在长方形材料
. 现要在长方形材料![]() 中裁剪出四边形材料
中裁剪出四边形材料![]() ,满足
,满足![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() ,
,![]() 上.
上.
(1)设![]() ,试将四边形材料
,试将四边形材料![]() 的面积表示为
的面积表示为![]() 的函数,并指明
的函数,并指明![]() 的取值范围;
的取值范围;
(2)试确定点![]() 在
在![]() 上的位置,使得四边形材料
上的位置,使得四边形材料![]() 的面积
的面积![]() 最小,并求出其最小值.
最小,并求出其最小值.
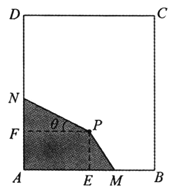
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“克拉茨猜想”又称“![]() 猜想”,是德国数学家洛萨·克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数
猜想”,是德国数学家洛萨·克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半;如果
是偶数,就将它减半;如果![]() 是奇数,就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.已知正整数
是奇数,就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.已知正整数![]() 经过7次运算后首次得到1,则
经过7次运算后首次得到1,则![]() 的所有不同取值的集合为____________.
的所有不同取值的集合为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com