
【题目】已知函数f(x)=x|x﹣a|,a∈R.
(1)当f(2)+f(﹣2)>4时,求a的取值范围;
(2)若a>0,x,y∈(﹣∞,a],不等式f(x)≤|y+3|+|y﹣a|恒成立,求a的取值范围.
【答案】(1)(﹣∞,﹣1)(2)0<a≤6
【解析】
(1)化简不等式![]() 得到
得到![]() ,利用零点分段法求得不等式的解集,也即求得
,利用零点分段法求得不等式的解集,也即求得![]() 的取值范围.
的取值范围.
(2)将不等式![]() 恒成立,转化为
恒成立,转化为![]() .求得
.求得![]() 的最大值以及
的最大值以及![]() 的最小值,由此列不等式,解不等式求得
的最小值,由此列不等式,解不等式求得![]() 的取值范围.
的取值范围.
(1)f(2)+f(﹣2)>4,可得2|2﹣a|﹣2|2+a|>4,即|a﹣2|﹣|a+2|>2,
则![]() 或
或![]() 或
或![]() ,
,
解得a≤﹣2或﹣2<a<﹣1或a∈,则a的范围是(﹣∞,﹣1);
(2)f(x)≤|y+3|+|y﹣a|恒成立,等价为f(x)max≤(|y+3|+|y﹣a|)min,
其中当x,y∈(﹣∞,a],|y+3|+|y﹣a|≥|y+3+a﹣y|=|a+3|=a+3,当且仅当﹣3≤y≤a取得等号,
而f(x)=﹣x(x﹣a)=﹣(x![]() )2
)2![]() ,当且仅当x
,当且仅当x![]() a时取得等号.
a时取得等号.
所以![]() a+3,解得0<a≤6.
a+3,解得0<a≤6.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=2y,过点(0,2)作直线l交抛物线于A、B两点.
(1)证明:OA⊥OB;
(2)若直线l的斜率为1,过点A、B分别作抛物线的切线l1,l2,若直线l1,l2,相交于点P,直线l1,l2交x轴分别于点M,N,求△MNP的外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①函数![]() 的图象把圆
的图象把圆![]() 的面积两等分
的面积两等分
②![]() 是周期为
是周期为![]() 的函数
的函数
③函数![]() 在区间
在区间![]() 上有3个零点
上有3个零点
④函数![]() 在区间
在区间![]() 上单调递减
上单调递减
其中所有正确结论的编号是( )
A.①③④B.②④C.①④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障某治疗新冠肺炎药品的主要药理成分在国家药品监督管理局规定的值范围内,武汉某制药厂在该药品的生产过程中,检验员在一天中按照规定从该药品生产线上随机抽取20件产品进行检测,测量其主要药理成分含量(单位:mg).根据生产经验,可以认为这条药品生产线正常状态下生产的产品的主要药理成分含量服从正态分布N(μ,σ2).在一天内抽取的20件产品中,如果有一件出现了主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对本次的生产过程进行检查.
(1)下面是检验员在2月24日抽取的20件药品的主要药理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 10.04 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 9.95 | 10.05 | 10.05 | 9.96 | 10.12 |
经计算得![]() xi=9.96,s
xi=9.96,s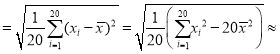 0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数
0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对本次的生产过程进行检查?
,利用估计值判断是否需对本次的生产过程进行检查?
(2)假设生产状态正常,记X表示某天抽取的20件产品中其主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品件数,求/span>P(X=1)及X的数学期望.
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ﹣3σ<Z<μ+3σ)≈0.9974,0.997419≈0.95.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设正整数m,n满足![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 为集各
为集各![]() 的n元子集,且
的n元子集,且![]() ;
;
(1)若![]() ,满足
,满足![]() ;
;
(i)求证:![]() ;
;
(ii)求满足条件的集合![]() 的个数;
的个数;
(2)若![]() 中至多有一个元素,求证:
中至多有一个元素,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.
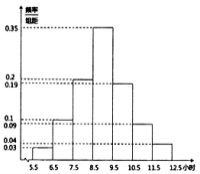
(1)求这200名学生每周阅读时间的样本平均数![]() 和中位数
和中位数![]() (
(![]() 的值精确到0.01);
的值精确到0.01);
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为![]() ,
,![]() 的学生中抽取9名参加座谈会.
的学生中抽取9名参加座谈会.
(i)你认为9个名额应该怎么分配?并说明理由;
(ii)座谈中发现9名学生中理工类专业的较多.请根据200名学生的调研数据,填写下面的列联表,并判断是否有![]() 的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
阅读时间不足8.5小时 | 阅读时间超过8.5小时 | |
理工类专业 | 40 | 60 |
非理工类专业 |
附:![]() (
(![]() ).
).
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于正整数![]() ,如果
,如果![]() 个整数
个整数![]() 满足
满足![]() ,
,
且![]() ,则称数组
,则称数组![]() 为
为![]() 的一个“正整数分拆”.记
的一个“正整数分拆”.记![]() 均为偶数的“正整数分拆”的个数为
均为偶数的“正整数分拆”的个数为![]() 均为奇数的“正整数分拆”的个数为
均为奇数的“正整数分拆”的个数为![]() .
.
(Ⅰ)写出整数4的所有“正整数分拆”;
(Ⅱ)对于给定的整数![]() ,设
,设![]() 是
是![]() 的一个“正整数分拆”,且
的一个“正整数分拆”,且![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)对所有的正整数![]() ,证明:
,证明:![]() ;并求出使得等号成立的
;并求出使得等号成立的![]() 的值.
的值.
(注:对于![]() 的两个“正整数分拆”
的两个“正整数分拆”![]() 与
与![]() ,当且仅当
,当且仅当![]() 且
且![]() 时,称这两个“正整数分拆”是相同的.)
时,称这两个“正整数分拆”是相同的.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】购买一辆某品牌新能源汽车,在行驶三年后,政府将给予适当金额的购车补贴.某调研机构对拟购买该品牌汽车的消费者,就购车补贴金额的心理预期值进行了抽样调查,其样本频率分布直方图如图所示
.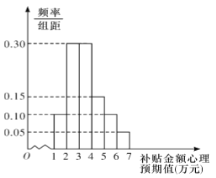
(1)估计拟购买该品牌汽车的消费群体对购车补贴金额的心理预期值的方差(同一组中的数据用该组区间的中点值作代表);
(2)将频率视为概率,从拟购买该品牌汽车的消费群体中随机抽取![]() 人,记对购车补贴金额的心理预期值高于
人,记对购车补贴金额的心理预期值高于![]() 万元的人数为
万元的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)统计最近![]() 个月该品牌汽车的市场销售量,得其频数分布表如下:
个月该品牌汽车的市场销售量,得其频数分布表如下:
月份 |
|
|
|
|
|
销售量(万辆) |
|
|
|
|
|
试预计该品牌汽车在![]() 年
年![]() 月份的销售量约为多少万辆?
月份的销售量约为多少万辆?
附:对于一组样本数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com