
【题目】“克拉茨猜想”又称“![]() 猜想”,是德国数学家洛萨·克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数
猜想”,是德国数学家洛萨·克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半;如果
是偶数,就将它减半;如果![]() 是奇数,就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.已知正整数
是奇数,就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.已知正整数![]() 经过7次运算后首次得到1,则
经过7次运算后首次得到1,则![]() 的所有不同取值的集合为____________.
的所有不同取值的集合为____________.
【答案】![]()
【解析】
由题,设第7次的运算结果为![]() ,分别讨论第6次为奇数和偶数的情况,即可推导第6次的结果,依次类推,经过7次运算后得到所求,求解过程中需注意,正整数
,分别讨论第6次为奇数和偶数的情况,即可推导第6次的结果,依次类推,经过7次运算后得到所求,求解过程中需注意,正整数![]() 经过7次运算后首次得到1,则运算过程中出现非正整数及1均不符合条件.
经过7次运算后首次得到1,则运算过程中出现非正整数及1均不符合条件.
由题,由正整数![]() 经过7次运算后首次得到1,即可设第7次的运算结果为
经过7次运算后首次得到1,即可设第7次的运算结果为![]() ,
,
若第6次为奇数,则![]() ,解得
,解得![]() ,不符合;
,不符合;
若第6次为偶数,则![]() ,解得
,解得![]() ;
;
若第5次为奇数,则![]() ,解得
,解得![]() ,不符合;
,不符合;
若第5次为偶数,则![]() ,解得
,解得![]() ;
;
若第4次为奇数,则![]() ,解得
,解得![]() ,不符合;
,不符合;
若第4次为偶数,则![]() ,解得
,解得![]() ;
;
若第3次为奇数,则![]() ,解得
,解得![]() ,不符合;
,不符合;
若第3次为偶数,则![]() ,解得
,解得![]() ;
;
若第2次为奇数,则![]() ,解得
,解得![]() ①;
①;
若第2次为偶数,则![]() ,解得
,解得![]() ②;
②;
第1次为奇数,则①![]() ,解得
,解得![]() ,不符合;②
,不符合;②![]() ,解得
,解得![]() ,不符合;
,不符合;
第1次为偶数,则①![]() ,解得
,解得![]() ③;②
③;②![]() ,解得
,解得![]() ④;
④;
若![]() 为奇数,则③
为奇数,则③![]() ,解得
,解得![]() ;④
;④![]() ,解得
,解得![]() ;
;
若![]() 为偶数,则③
为偶数,则③![]() ,解得
,解得![]() ;④
;④![]() ,解得
,解得![]() .
.
综上,![]() 的所有不同取值的集合为
的所有不同取值的集合为![]() ,
,
故答案为:![]()


科目:高中数学 来源: 题型:
【题目】购买一辆某品牌新能源汽车,在行驶三年后,政府将给予适当金额的购车补贴.某调研机构对拟购买该品牌汽车的消费者,就购车补贴金额的心理预期值进行了抽样调查,其样本频率分布直方图如图所示
.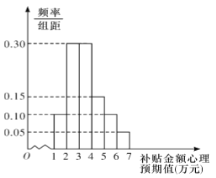
(1)估计拟购买该品牌汽车的消费群体对购车补贴金额的心理预期值的方差(同一组中的数据用该组区间的中点值作代表);
(2)将频率视为概率,从拟购买该品牌汽车的消费群体中随机抽取![]() 人,记对购车补贴金额的心理预期值高于
人,记对购车补贴金额的心理预期值高于![]() 万元的人数为
万元的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)统计最近![]() 个月该品牌汽车的市场销售量,得其频数分布表如下:
个月该品牌汽车的市场销售量,得其频数分布表如下:
月份 |
|
|
|
|
|
销售量(万辆) |
|
|
|
|
|
试预计该品牌汽车在![]() 年
年![]() 月份的销售量约为多少万辆?
月份的销售量约为多少万辆?
附:对于一组样本数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的标号为( )
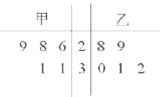
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,
中,![]() 是过定点
是过定点![]() 且倾斜角为
且倾斜角为![]() 的直线;在极坐标系(以坐标原点
的直线;在极坐标系(以坐标原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴,取相同单位长度)中,曲线
轴非负半轴为极轴,取相同单位长度)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的参数方程,并将曲线
的参数方程,并将曲线![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)若曲线![]() 与直线
与直线![]() 相交于不同的两点
相交于不同的两点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次不等式ax2+x+b>0的解集为(-∞,-2)∪(1,+∞).
(Ⅰ)求a和b的值;
(Ⅱ)求不等式ax2-(c+b)x+bc<0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,
,![]() 为椭圆的下顶点,
为椭圆的下顶点,![]() 交椭圆于另一点
交椭圆于另一点![]() 、
、![]() 的面积
的面积![]() .
.
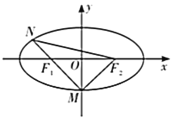
(1)求椭圆的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,问:直线
,问:直线![]() 是否过定点?若是,请求出定点的坐标;若不是,请说明理由.
是否过定点?若是,请求出定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 的顶点,
的顶点,![]() ,
,![]() 是
是![]() 上的两个动点,且
上的两个动点,且![]() .
.
(1)判断点![]() 是否在直线
是否在直线![]() 上?说明理由;
上?说明理由;
(2)设点![]() 是△
是△![]() 的外接圆的圆心,点
的外接圆的圆心,点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,点
,点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为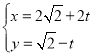 (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)把曲线![]() 向下平移
向下平移![]() 个单位,然后各点横坐标变为原来的
个单位,然后各点横坐标变为原来的![]() 倍得到曲线
倍得到曲线![]() (纵坐标不变),设点
(纵坐标不变),设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com