
 如图所示,平面ABC⊥平面BCD,△ABC为正三角形,且AB=2,BC⊥CD,点E为棱AC的中心.
如图所示,平面ABC⊥平面BCD,△ABC为正三角形,且AB=2,BC⊥CD,点E为棱AC的中心.分析 (1)先利用题中所给的平面与平面垂直以及直线与直线垂直,判断得到直线与平面垂直,然后利用平面与平面垂直的判定定理证明面面垂直;
(2)利用给定的直线与平面所成的角,计算得到棱CD的长,并依据图形建立空间直角坐标系,利用相关点的坐标计算得到相应平面的法向量,然后利用法向量求二面角的余弦值.
解答 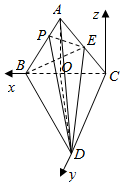 证明:(1)因为点E为棱AC的中点,△ABC为正三角形,
证明:(1)因为点E为棱AC的中点,△ABC为正三角形,
所以BE⊥AC.
因为平面ABC⊥平面BCD,BC⊥CD,平面ABC∩平面BCD=BC,
所以CD⊥平面ABC.
因为BE?平面ABC,所以CD⊥BE.
又AC∩CD=C,所以BE⊥平面ACD.
又BE?平面BED,所以平面BED⊥平面ACD.
解:(2)过点A作AO⊥BC,交BC于点O,则点O为BC的中点.
连接OD,
因为平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,
所以AO⊥平面BCD,
所以∠ADO为直线AD与平面BCD所成的角.
在Rt△AOD中,AO=$\sqrt{3}$,所以sin∠ADO=$\frac{AO}{AD}=\frac{\sqrt{3}}{AD}=\frac{\sqrt{3}}{4}$,所以AD=4.
在△ACD中,AC⊥CD,AC=2,所以CD=2$\sqrt{3}$.
以点C为坐标原点,CB为x轴,CD为y轴,过C作平面BCD的垂线为z轴,
建立如图所示的空间直角坐标系C-xyz.
则A(1,0,$\sqrt{3}$),E($\frac{1}{2}$,0,$\frac{\sqrt{3}}{2}$),D(0,2$\sqrt{3}$,0),B(2,0,0),
所以$\overrightarrow{BE}$=(-$\frac{3}{2}$,0,$\frac{\sqrt{3}}{2}$),$\overrightarrow{DE}$=($\frac{1}{2}$,-2$\sqrt{3}$,$\frac{\sqrt{3}}{2}$).
因为$\overrightarrow{AB}$=3$\overrightarrow{AP}$,所以P($\frac{4}{3}$,0,$\frac{2\sqrt{3}}{3}$),$\overrightarrow{DP}$=($\frac{4}{3}$,-2$\sqrt{3}$,$\frac{2\sqrt{3}}{3}$).
设平面BED的法向量为$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BE}=-\frac{3}{2}x+\frac{\sqrt{3}}{2}z=0}\\{\overrightarrow{m}•\overrightarrow{DE}=\frac{1}{2}x-2\sqrt{3}y+\frac{\sqrt{3}}{2}z=0}\end{array}\right.$,令y=1,则x=$\sqrt{3}$,z=3,
所以$\overrightarrow{m}$=($\sqrt{3}$,1,3)为平面BED的一个法向量.
设平面PED的法向量为$\overrightarrow{n}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=\frac{1}{2}a-2\sqrt{3}b+\frac{\sqrt{3}}{2}c=0}\\{\overrightarrow{n}•\overrightarrow{DP}=\frac{4}{3}a-2\sqrt{3}b+\frac{2\sqrt{3}}{3}c=0}\end{array}\right.$,令b=1,则a=-$\sqrt{3}$,c=5,
得平面PED的一个法向量为$\overrightarrow{n}$=(-$\sqrt{3}$,1,5).
设二面角P-DE-B的大小为θ,由图易知二面角P-DE-B为锐角,
则cos θ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{|-3+1+15|}{\sqrt{13}•\sqrt{29}}$=$\frac{\sqrt{377}}{29}$,
即二面角P-DE-B的余弦值为$\frac{\sqrt{377}}{29}$.
点评 本题主要考查空间平面与平面垂直的证明以及直线与平面、平面与平面所成角的求解,立体几何试题每年都考,难度中等偏上,常常考查有关线面平行、垂直的证明以及线面角和二面角的相关计算,从近几年的考情来看,有关线面平行、垂直的证明以几何推理为主,而空间角的计算则较多的考查利用空间向量法求解.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知SA⊥正方形ABCD所在平面,O为AC与BD的交点.
如图所示,已知SA⊥正方形ABCD所在平面,O为AC与BD的交点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在直角△ABC中,AB⊥BC,D为BC的中点,以AB为直径作圆O,分别交AC、AD于点E,F,若AF=3,FD=1,则AE等于( )
如图,在直角△ABC中,AB⊥BC,D为BC的中点,以AB为直径作圆O,分别交AC、AD于点E,F,若AF=3,FD=1,则AE等于( )| A. | $\sqrt{6}$ | B. | $\frac{6\sqrt{7}}{7}$ | C. | $\frac{8\sqrt{7}}{7}$ | D. | $\frac{4\sqrt{21}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
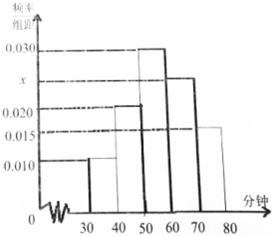 4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,并用简单随机抽样方法抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”
4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,并用简单随机抽样方法抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”| 非读书迷 | 读书迷 | 合计 | |
| 男 | 15 | ||
| 女 | 45 | ||
| 合计 |
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{{{42}^5}}}$ | B. | $\frac{1}{{{{42}^4}}}$ | C. | $\frac{{A}_{42}^{5}}{4{2}^{5}}$ | D. | $\frac{{P_{42}^4}}{{{{42}^5}}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com