
分析 (1)根据等差数列前n项和公式$\frac{({a}_{1}+{a}_{6})×6}{2}$=$\frac{{(a}_{1}+{a}_{15})×15}{2}$,将a1=20,即可求得公差d,根据等差数列通项公式即可求得{an}的通项公式;
(2)根据二次函数图象对称确定,当n=11,a11=0,可知n=10或11时,S10=S11,Sn取得最大值,根据等差数列前n项和公式,即可求得Sn取得最大值;
(3)由题意可知当n≤11时,an≥0,求得Tn,当n≥12时,an<0根据数列的性质,可知Tn=2S11-(21n-n2)=n2-21n+220,即可求得数列{|an|}的前n项和Tn.
解答 解:(1)由题意可知:S6=S15,即$\frac{({a}_{1}+{a}_{6})×6}{2}$=$\frac{{(a}_{1}+{a}_{15})×15}{2}$,
∴2a6=3a1+5a15,
∴2(a1+5d)=3a1+5(a1+14d),
解得:d=-2,
∴an=20+(-2)(n-1)=22-2n,
∴{an}的通项公式an=22-2n;
(2)由题意可知,S6=S15,
∴Sn=f(n)的对称轴方程为:n=$\frac{6+15}{2}$=10.5,
10.5∉N*,
∴n=10或11时,S10=S11,
∴a11=0,d<0,
∴S10=S11=$\frac{(20+0)×11}{2}$=110,
Sn最大值为110.
(3)由题意可知:a11=0,
∴当n≤11时,an≥0,
Tn=$\frac{(20+22-2n)n}{2}$=21n-n2,
当n≥12时,an<0,
Tn=2S11-(21n-n2)=n2-21n+220,
∴${S_n}=\left\{\begin{array}{l}21n-{n^2},1≤n≤11\\ 220-21n+{n^2},n≥12.\end{array}\right.$.
点评 本题考查等差数列的通项公式及前n项和公式,考查等差数列前n项和公式的性质及其图象,考查含绝对值数列的前n项和公式的求法,属于中档题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
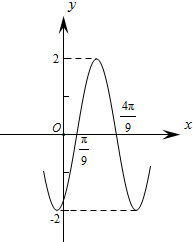
| A. | 函数f(x)的最小正周期为$\frac{π}{2}$ | B. | φ=$\frac{π}{9}$ | ||
| C. | 函数f(x)的图象关于直线x=$\frac{5π}{6}$对称 | D. | 函数f(x)在区间[0,$\frac{π}{4}$]上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 48 | C. | 42 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com