【答案】
分析:令f(x)=cosx+lnx
2(x≠0),可得f(-x)=f(x),f(x)是偶函数,其图象关于y轴对称.利用导数
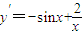
(x≠0),可知:当2>x>0时,y′>0.及f(π)=-1+2lnπ>0即可判断出.
解答:解:令f(x)=cosx+lnx
2(x≠0),则f(-x)=f(x),即f(x)是偶函数,其图象关于y轴对称.
∵
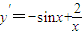
(x≠0),∴当2>x>0时,y′>0.
由f(π)=-1+2lnπ>0
可知:只有A适合.
故选A.
点评:熟练掌握偶函数的性质、利用导数研究函数的单调性、数形结合的思想方法等是解题的关键.





 阅读快车系列答案
阅读快车系列答案